
【题目】如图,线段AB=6cm,动点P以2cm/s的速度从A﹣B﹣A在线段AB上运动,到达点A后,停止运动;动点Q以1cm/s的速度从B﹣A在线段AB上运动,到达点A后,停止运动.若动点P,Q同时出发,设点Q的运动时间是t(单位:s)时,两个动点之间的距离为S(单位:cm),则能表示S与t的函数关系的是( )
![]()
A. B.
B.
C. D.
D.
【答案】D
【解析】
分别分三个阶段计算和分析两动点之间距离与时间的关系:①P、Q从出发到第一次相遇;②从P、Q第一次相遇到P点到达B地;③从动点P到达点B到动点P返回点A,据此求解.
设点Q的运动时间是t(单位:s)时,两个动点之间的距离为S(单位:cm),
P、Q从出发到第一次相遇:
6=2t+t
解得,t=2
由此可知,刚开始P和Q两点间的距离越来越小直到相遇时,它们之间的距离变为0,此时用的时间为2s;
此时,点P离点B的距离为:6﹣2×2=2cm,点Q离点A的距离为:6﹣2=4cm,
相遇后,点P到达B点用的时间为:2÷2=1s,此时两个动点之间的距离为3cm,
由此可知,相遇后,在第3s时点P到达B点,从相遇到点P到达B点它们的距离在变大,1s后P点从B点返回,点P继续运动,两个动点之间的距离逐渐变小,同时达到A点.
故选:D.


科目:初中数学 来源: 题型:
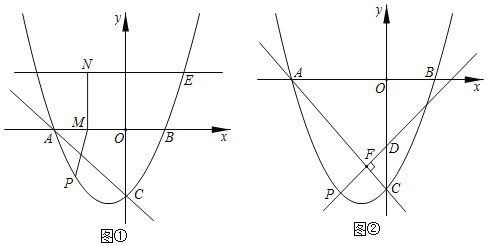
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,抛物线上的点
,抛物线上的点![]() 的横坐标为3,过点
的横坐标为3,过点![]() 作直线
作直线![]() 轴.
轴.
(1)点![]() 为抛物线上的动点,且在直线
为抛物线上的动点,且在直线![]() 的下方,点
的下方,点![]() ,
,![]() 分别为
分别为![]() 轴,直线
轴,直线![]() 上的动点,且
上的动点,且![]() 轴,当
轴,当![]() 面积最大时,求
面积最大时,求![]() 的最小值;
的最小值;
(2)过(1)中的点![]() 作
作![]() ,垂足为
,垂足为![]() ,且直线
,且直线![]() 与
与![]() 轴交于点
轴交于点![]() ,把
,把![]() 绕顶点
绕顶点![]() 旋转45°,得到
旋转45°,得到![]() ,再把
,再把![]() 沿直线
沿直线![]() 平移至
平移至![]() ,在平面上是否存在点
,在平面上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在直接写出点
为顶点的四边形为菱形?若存在直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ![]() ,点A,B,E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )
,点A,B,E在x轴上,若正方形BEFG的边长为6,则点C的坐标为( )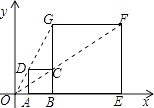
A.(2,2)
B.(3,1)
C.(3,2)
D.(4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的爱国意识,某中学举办“爱我中华”朗诵比赛,全校学生都参加,并对表现优异的学生进行表彰,设置一、二、三等奖和进步奖共四个奖项,赛后,校统计小组随机抽取了九年级两个班级,并将这两个班的获奖情况绘制成以下两幅不完整的统计图.
请根据图中的信息,解答下列问题:
(1)求本次调查抽取的学生人数,并补全条形统计图;
(2)在扇形统计图中,表示“三等奖”的扇形所对应的圆心角度数是 72 °.
(3)若该校共有2600名学生,试估计得奖的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一枚质地均匀的正四面体骰子,它的四个面上分别标有数字0,1,2,3,如图2,正方形ABCD的四个顶点处均有一个圈.课间,李丽和王萍利用它们玩跳圈游戏,玩法如下:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形ABCD的边顺时针分钟连续跳几个边长.
例如:若从圈A起跳,第一掷得的数字为2,便沿正方形的边顺时针连续跳2个边长,落到圈C,第二次掷得的数字为3,便从圈C开始,沿正方形的边顺时针连续跳3个边长,落到圈B,….
设她们从圈A起跳.
(1)若李丽随机掷这枚骰子一次,求她跳回圈A的概率;
(2)若王萍随机掷这枚骰子两次,请用列表法或画树状图求她最后跳回圈A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们经常利用图形描述问题和分析问题.借助直观的几何图形,把问题变得简明、形象,有助于探索解决问题的思路.
(1)在整式乘法公式的学习中,小明为了解释某一公式,构造了几何图形,如图1所示,先画了边长为a,b的大小两个正方形,再延长小正方形的两边,把大正方形分割为四部分,并分别标记为Ⅰ,Ⅱ,Ⅲ,Ⅳ,然后补出图形Ⅴ.显然图形Ⅴ与图形Ⅳ的面积相等,所以图形Ⅰ,Ⅱ,Ⅴ的面积和与图形Ⅰ,Ⅱ,Ⅳ的面积和相等,从而验证了公式.则小明验证的公式是 ;

(2)计算:(x+a)(x+b)= ;请画图说明这个等式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com