
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC上,且BE=BD,连接AE、DE、DC.若∠CAE=30°,则∠BDC=_____.

【答案】75°
【解析】
延长AE交DC边于点F,先判定Rt△ABE≌Rt△CBD(HL),由全等三角形的性质可得∠AEB=∠BDC,AB=BC,则∠BAC=∠ACB=45°,再由∠AEB为△AEC的外角,可求得∠AEB的度数,即∠BDC的度数.
解:延长AE交DC边于点F,如图:

∵∠ABC=90°,
∴∠CBD=90°,
在Rt△ABE与Rt△CBD中,![]()
∴Rt△ABE≌Rt△CBD(HL),
∴∠AEB=∠BDC,AB=BC,
∴∠BAC=∠ACB=45°,
∵∠AEB为△AEC的外角,∠CAE=30°,
∴∠AEB=∠ACB+∠CAE=45°+30°=75°,
∴∠BDC=75°.
故答案为:75°.


科目:初中数学 来源: 题型:
【题目】探究:22﹣21=2×21﹣1×21=2( )
23﹣22= =2( ),
24﹣23= =2( ),
……
(1)请仔细观察,写出第4个等式;
(2)请你找规律,写出第n个等式;
(3)计算:21+22+23+…+22019﹣22020.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块矩形木板,木工采用如图的方式,在木板上截出两个面积分别为18dm2和32dm2的正方形木板.

(1)求剩余木料的面积.
(2)如果木工想从剩余的木料中截出长为1.5dm,宽为ldm的长方形木条,最多能截出 块这样的木条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一幅三角板按如图所示的方式放置,则下列结论中不正确的是( )

A. ∠1=∠3 B. 如果∠2=30°,则有AC∥DE
C. 如果∠2=30°,则有BC∥AD D. 如果∠2=30°,必有∠4=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
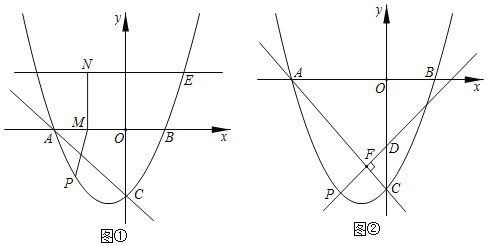
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,抛物线上的点
,抛物线上的点![]() 的横坐标为3,过点
的横坐标为3,过点![]() 作直线
作直线![]() 轴.
轴.
(1)点![]() 为抛物线上的动点,且在直线
为抛物线上的动点,且在直线![]() 的下方,点
的下方,点![]() ,
,![]() 分别为
分别为![]() 轴,直线
轴,直线![]() 上的动点,且
上的动点,且![]() 轴,当
轴,当![]() 面积最大时,求
面积最大时,求![]() 的最小值;
的最小值;
(2)过(1)中的点![]() 作
作![]() ,垂足为
,垂足为![]() ,且直线
,且直线![]() 与
与![]() 轴交于点
轴交于点![]() ,把
,把![]() 绕顶点
绕顶点![]() 旋转45°,得到
旋转45°,得到![]() ,再把
,再把![]() 沿直线
沿直线![]() 平移至
平移至![]() ,在平面上是否存在点
,在平面上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在直接写出点
为顶点的四边形为菱形?若存在直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商人制成了一个如图所示的转盘,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖励3元;若指针指向字母“C”,则奖励1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.AO交⊙O于点E,延长AO交⊙O于点D,tanD= ![]() ,
,
(1)求 ![]() 的值.
的值.
(2)设⊙O的半径为3,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一枚质地均匀的正四面体骰子,它的四个面上分别标有数字0,1,2,3,如图2,正方形ABCD的四个顶点处均有一个圈.课间,李丽和王萍利用它们玩跳圈游戏,玩法如下:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形ABCD的边顺时针分钟连续跳几个边长.
例如:若从圈A起跳,第一掷得的数字为2,便沿正方形的边顺时针连续跳2个边长,落到圈C,第二次掷得的数字为3,便从圈C开始,沿正方形的边顺时针连续跳3个边长,落到圈B,….
设她们从圈A起跳.
(1)若李丽随机掷这枚骰子一次,求她跳回圈A的概率;
(2)若王萍随机掷这枚骰子两次,请用列表法或画树状图求她最后跳回圈A的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com