
【题目】如图,两个形状、大小完全相同的含有30。角的直角三角板如图1放置,PA、PB与直线MN重合,且三角板PAC和三角板PBD均可以绕点P逆时针旋转.
(1)如图1.则∠DPC为多少度?
(2)如图2,若三角板PAC的边PA从PN处开始绕点P逆时针旋转的角度为α,PF平分∠APD,PE平分∠CPD,求∠EPF的度数;
(3)如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3。/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2。/秒,在两个三角板旋转过程中,当PC转到与PM重合时,两个三角板都停止转动.设两个三角板旋转时间为t秒,请问 ![]() 是定值吗?若是定值,请求出这个定值;若不是定值,请说明理由。
是定值吗?若是定值,请求出这个定值;若不是定值,请说明理由。
【答案】
(1)解:∵∠DPC=180°-∠CPA-∠DPB,∠CPA=60°,∠DPB=30°,
∴∠DPC=180゜-30゜-60゜=90゜
(2)
(3)解: ![]() 是定值,理由如下:
是定值,理由如下:
设运动时间为t秒 ![]() ,则∠NPA=3t,∠MPB=2t,
,则∠NPA=3t,∠MPB=2t,
∴∠BPN=1800-2t,
∠CPD=3600-∠DPB-∠BPN-∠NPA-∠CPA=900-t,
∴ ![]()
【解析】(1)利用含有30゜、60゜的三角板得出∠DPC=180°-∠CPA-∠DPB,代入计算即可;
(2)根据角平分线的定义得出∠DPF=![]() ∠APD,∠DPE=
∠APD,∠DPE=![]() ∠CPD ,根据角的和差得出APD=180°30°α=150°α ,∠CPD=180°30°60°α=90°α ,从而得出∠DPF及,∠DPE的度数,最后根据EPF=∠DPF∠DPE算出结果;
∠CPD ,根据角的和差得出APD=180°30°α=150°α ,∠CPD=180°30°60°α=90°α ,从而得出∠DPF及,∠DPE的度数,最后根据EPF=∠DPF∠DPE算出结果;
(3)首先得出![]() 是一个定值, 设运动时间为t秒,则∠BPM=2t,∠NPA=3t ,∠BPN=1800-2t ,∠CPD=3600-∠DPB-∠BPN-∠NPA-∠CPA=900-t ,即可得出答案.
是一个定值, 设运动时间为t秒,则∠BPM=2t,∠NPA=3t ,∠BPN=1800-2t ,∠CPD=3600-∠DPB-∠BPN-∠NPA-∠CPA=900-t ,即可得出答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
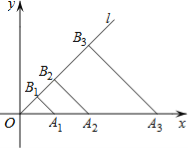
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在x轴的正半轴上,且OA1=2,OA2=2OA1,OA3=2OA2,…,OAn=2OAn﹣1,点B1,B2,B3,…,Bn在第一象限的角平分线l上,且A1B1,A2B2,…,AnBn都与射线l垂直,则B1的坐标是 ,B3的坐标是 ,Bn的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况,并将所得数据进行了统计,结果如图所示.
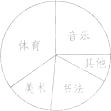
(1)在这次调查中,一共抽查了多少名学生?
(2)求出扇形统计图中参加“音乐”活动项目所对应的扇形的圆心角度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( ) 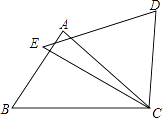
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=EC,∠A=∠D
D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
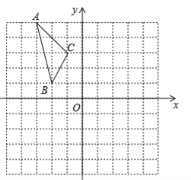
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;
(2)若△ABC和△A1B2C2关于原点O成中心对称图形,写出△A1B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A2B3C3,写出△A2B3C3的各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上. 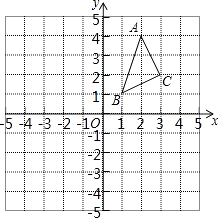
(1)画出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标;
(2)画出△ABC关于y轴对称的△A2B2C2 , 并写出点B2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com