
【题目】如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE.请说明EF平分∠AED.

【答案】见解析.
【解析】
先利用角平分线定义得到∠ABD=∠CBD,再根据平行线的性质由ED∥BC得∠EDB=∠CBD,则∠ABD=∠EDB,接着由∠FED=∠BDE可判断EF∥BD,则利用平行线的性质得∠EDB=∠DEF,∠ABD=∠AEF,所以∠AEF=∠DEF,从而得到结论.
∵BD是∠ABC的平分线(已知),
∴∠ABD=∠DBC(角平分线的定义).
∵ED∥BC(已知),
∴∠BDE=∠DBC(两直线平行,内错角相等),
∴∠ABD=∠BDE(等量代换).
又∵∠FED=∠BDE(已知),
∴EF∥BD(内错角相等,两直线平行),∠FED=∠ABD(等量代换),
∴∠AEF=∠ABD(两直线平行,同位角相等),
∴∠AEF=∠FED(等量代换),
∴EF平分∠AED(角平分线的定义).


科目:初中数学 来源: 题型:
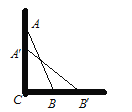
【题目】一架长2.5米的梯子AB如图所示斜靠在一面墙上,这时梯足B离墙底C(∠C=90°)的距离BC为0.7米.
(1)求此时梯顶A距地面的高度AC;
(2)如果梯顶A下滑0.9米,那么梯足B在水平方向,向右滑动了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.则下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP.其中正确的是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60,得到△BAE,连接ED,若BC=5,BD=4,则有以下四个结论:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC。其中正确结论的序号是( )
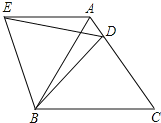
A. ②③④ B. ①③④ C. ①②④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D, AB=AD.
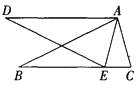
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为直径,点C为圆上一点,将劣弧 ![]() 沿弦AC翻折交AB于点D,连结CD.
沿弦AC翻折交AB于点D,连结CD. 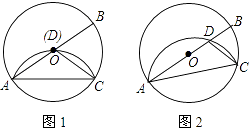
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y= ![]() x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M10的坐标为 .
x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M10的坐标为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com