
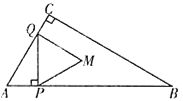
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发以每秒2个单位的速度沿
出发以每秒2个单位的速度沿![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 的垂线交折线
的垂线交折线![]() 于点
于点![]() ,当点
,当点![]() 不和
不和![]() 的顶点重合时,以
的顶点重合时,以![]() 为边作等边三角形
为边作等边三角形![]() ,使点
,使点![]() 和点
和点![]() 在直线
在直线![]() 的同侧,设点
的同侧,设点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).
(1)求等边三角形![]() 的边长(用含
的边长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 的边
的边![]() 上时,求
上时,求![]() 的值;
的值;
(3)设![]() 与
与![]() 重合部分图形的面积为
重合部分图形的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)作直线![]() ,设点
,设点![]() 关于直线
关于直线![]() 的对称点分别为
的对称点分别为![]() ,直接写出
,直接写出![]() 时
时![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)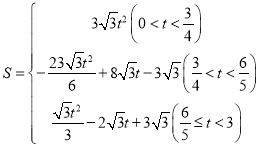 ;(4)
;(4)![]() 的值为
的值为![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)分两种情况讨论:当点Q在线段AC上时,当点Q在线段BC上时,根据30度的直角三角形的性质或特殊的三角函数列式可得结论;
(2)根据PQ=PM,列出关于t的方程即可解答;
(3)分三种情况:①当![]() 时,Q在AC上,如图2,△PQM与△ABC重合部分图形是等边△PMQ,
时,Q在AC上,如图2,△PQM与△ABC重合部分图形是等边△PMQ,
②当![]() 时,Q在BC上,如图5,△PQM与△ABC重合部分图形是四边形PEDQ,
时,Q在BC上,如图5,△PQM与△ABC重合部分图形是四边形PEDQ,
③当![]() 时,Q在BC上,如图4,△PQM与△ABC重合部分图形是等边△PMQ,
时,Q在BC上,如图4,△PQM与△ABC重合部分图形是等边△PMQ,
根据面积公式可得结论;
(4)分两种情况:
①当Q在AC上时,如图6,根据AC=AQ+CQ,列关于t的方程可得结论;
当Q在BC上时,如图7,根据CQ=Q'E=2PQ,列关于t的方程可得结论.
解:(1)由题意,得![]() ,在
,在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,当点
,当点![]() 与点
与点![]() 重合时,如图①,
重合时,如图①,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,当点
,当点![]() 在边
在边![]() 上时,如图②,
上时,如图②,
即![]()
当点![]() 在边
在边![]() 上时,如图③,即
上时,如图③,即![]() ,
,
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ;
;
(2)当点![]() 落在
落在![]() 上时,如图④,
上时,如图④,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)分三种情况:①当![]() 时,点
时,点![]() 在
在![]() 上,如图②,
上,如图②,![]() 与
与![]() 重合部分图形是等边
重合部分图形是等边![]() ,
,
∴![]() ;
;
②当![]() 时,点
时,点![]() 在
在![]() 上,如图⑤,
上,如图⑤,![]() 与
与![]() 重合部分图形是四边形
重合部分图形是四边形![]() ,
,
由(2)得,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴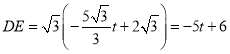 ,
,
∴![]()
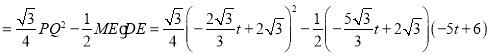
![]()
③当![]() 时,点
时,点![]() 在
在![]() 上,如图④,
上,如图④,![]() 与
与![]() 重合部分图形是等边
重合部分图形是等边![]() ,
,
∴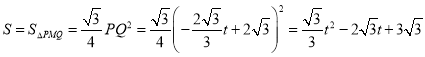
综上所述,![]() 与
与![]() 的函数关系式为
的函数关系式为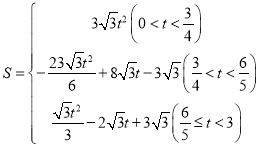
(4)分两种情况:
①当点![]() 在
在![]() 上时,如图⑥,
上时,如图⑥,![]() ,延长
,延长![]() 、
、![]() 交
交![]() 于同一点
于同一点![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
由对称得:![]() ,
,
∴![]() ,
,![]() 中,
中,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
②当点![]() 在
在![]() 上时,如图⑦,当
上时,如图⑦,当![]() 时,点
时,点![]() 在
在![]() 上,连接
上,连接![]() ,并延长
,并延长![]() 、
、![]() 交
交![]() 上同一点为
上同一点为![]() ,易得
,易得![]() ,
,
∴![]() ,由(2)知
,由(2)知![]() ,
,
∴![]() ,由
,由![]() 得
得![]() ,
,
解得![]() ,则
,则![]() 时
时![]() 的值为
的值为![]() 秒或
秒或![]() 秒.
秒.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】定义:(一)如果两个函数y1,y2,存在x取同一个值,使得y1=y2,那么称y1,y2为“合作函数”,称对应x的值为y1,y2的“合作点”;
(二)如果两个函数为y1,y2为“合作函数”,那么y1+y2的最大值称为y1,y2的“共赢值”.
(1)判断函数y=x+2m与y=![]() 是否为“合作函数”,如果是,请求出m=1时它们的合作点;如果不是,请说明理由;
是否为“合作函数”,如果是,请求出m=1时它们的合作点;如果不是,请说明理由;
(2)判断函数y=x+2m与y=3x﹣1(|x|≤2)是否为“合作函数”,如果是,请求出合作点;如果不是,请说明理由;
(3)已知函数y=x+2m与y=x2﹣(2m+1)x+(m2+4m﹣3)(0≤x≤5)是“合作函数”,且有唯一合作点.
①求出m的取值范围;
②若它们的“共赢值”为24,试求出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
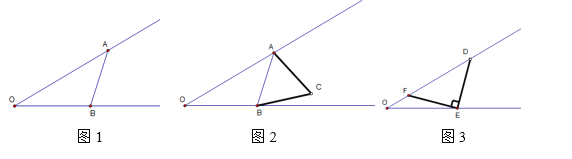
【题目】当一个角固定不变,而某种图形在该角的内部变化,则我们称这个角为墙角.
(1)如图1,墙角![]() =30°,如果AB=3,长度不变,在角内滑动,当OA=6时,则求出此时OB的长度.
=30°,如果AB=3,长度不变,在角内滑动,当OA=6时,则求出此时OB的长度.
(2)如图2,墙角![]() =30°,如果在AB的右边作等边
=30°,如果在AB的右边作等边![]() ,AB=3,长度不变,滑动过程中,请求出点O与点C的最大距离.
,AB=3,长度不变,滑动过程中,请求出点O与点C的最大距离.
(3)如图3,墙角![]() =
=![]() 时,如果点E是
时,如果点E是![]() 一条边上的一个点,
一条边上的一个点,![]() =90°,其两条边与
=90°,其两条边与![]() 另一条边交于点F与点D,求
另一条边交于点F与点D,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数且
为常数且![]() )中,当
)中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .请对该函数及其图像进行如下探究:
.请对该函数及其图像进行如下探究:
(1)求该函数的解析式,并直接写出该函数自变量![]() 的取值范围:
的取值范围:
(2)请在下列直角坐标系中画出该函数的图像:
列表如下:
x | … | -4 | -3 | -2 | -1 | 0 |
|
| 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | … |
描点连线:
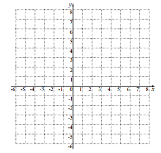
(3)请结合所画函数图象,写出函数图象的两条性质
(4)请你在上方直角坐标系中画出函数![]() 的图像,结合上述函数的图像,写出不等式
的图像,结合上述函数的图像,写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教委为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,启动了“学生阳光体育运动”,其中有一项是短跑运动,短跑运动可以锻炼人的灵活性,增强人的爆发力,因此张明和李亮在课外活动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
成绩统计分析表
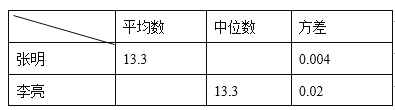
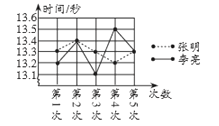
(1)张明第2次的成绩为__________秒;
(2)请补充完整上面的成绩统计分析表;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁? 请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于给定的两个函数![]() 和
和![]() ,我们把
,我们把![]() 叫做这个两个函数的积函数,把直线
叫做这个两个函数的积函数,把直线![]() 和
和![]() 叫做抛物线
叫做抛物线![]() 的母线.
的母线.
(1)直接写出函数![]() 和
和![]() 的积函数;
的积函数;
(2)点![]() 在(1)中的抛物线上,过点
在(1)中的抛物线上,过点![]() 垂直于
垂直于![]() 轴的直线分别交此抛物线的母线于
轴的直线分别交此抛物线的母线于![]() 两点(
两点(![]() 点不重合),设点
点不重合),设点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 时
时![]() 的值;
的值;
(3)已知函数![]() 和
和![]() .
.
①当它们的积函数自变量的取值范围是![]() ,且当
,且当![]() 时,这个积函数的最大值是8,求
时,这个积函数的最大值是8,求![]() 的值以及这个积函数的最小值;
的值以及这个积函数的最小值;
②当它们的积函数自变量的取值范围是![]() 时,直接写出这个积函数的图象在变化过程中最高点的纵坐标
时,直接写出这个积函数的图象在变化过程中最高点的纵坐标![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上(不与
上(不与![]() ,
,![]() 重合)的一个动点,过点
重合)的一个动点,过点![]() 作
作![]() 且
且![]() 交边
交边![]() 于点
于点![]() .
.
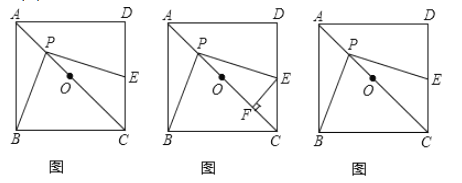
(1)求证:![]() .
.
(2)如图②,若正方形![]() 的边长为2,过
的边长为2,过![]() 作
作![]() 于点
于点![]() ,在
,在![]() 点运动的过程中,
点运动的过程中,![]() 的长度是否发生变化?若不变,试求出这个不变的值;若变化,请说明理由.
的长度是否发生变化?若不变,试求出这个不变的值;若变化,请说明理由.
(3)如图③,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 有两个不同的交点.下列结论:①
有两个不同的交点.下列结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则
有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则![]() ;其中正确的结论的个数是( )
;其中正确的结论的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:![]() . 设这种产品每天的销售利润为w元.
. 设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com