Question

4．有一抛物线型隧道，隧道最大高度为6m，跨度为8m．如图所示．
（1）求这条抛物线的解析式；
（2）当隧道过水时的水位只有OC的一半时，求水面宽度DF．

Answer 1

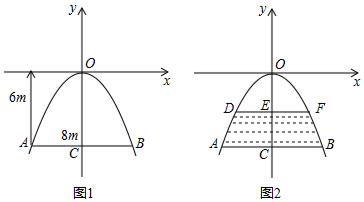
分析 （1）根据题意可以设出抛物线的解析式，由抛物线过点（4，-6），从而可以求得抛物线的解析式；
（2）将y=-3代入（1）中的解析式即可解答本题．

解答 解：（1）设抛物线的解析式为y=ax²，
∵点（4，-6）在此抛物线上，
∴-6=a×4²，
解得，a=-$\frac{3}{8}$，
即这条抛物线的解析式是y=-$\frac{3}{8}$x²；
（2）当y=-3时，
-3=-$\frac{3}{8}$x²，
解得，x=±$2\sqrt{2}$，
∴水面宽度DF为：$2\sqrt{2}-（-2\sqrt{2}）=4\sqrt{2}$m，
即当隧道过水时的水位只有OC的一半时，水面宽度DF为4$\sqrt{2}$m．

点评 本题考查二次函数的应用，解题的关键是明确题意，找出所求问需要的条件．