
【题目】已知关于 x 的一元二次方程 x![]() 2k 1 x k
2k 1 x k![]() k 1 0 有实数根.
k 1 0 有实数根.
(1)求k 的取值范围;
(2)若此方程的两实数根![]() ,
,![]() 满足
满足![]()
![]() 11 ,求k 的值.
11 ,求k 的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据方程有实数根得出△=[-(2k-1)]2-4×1×(k2+k-1)=-8k+5≥0,解之可得.
(2)利用根与系数的关系可用k表示出x1+x2和x1x2的值,根据条件可得到关于k的方程,可求得k的值,注意利用根的判别式进行取舍.
解:(1)∵关于x的一元二次方程x2-(2k-1)x+k2+k-1=0有实数根,
∴△≥0,即[-(2k-1)]2-4×1×(k2+k-1)=-8k+5≥0,
解得k≤![]() .
.
(2)由根与系数的关系可得x1+x2=2k-1,x1x2=k2+k-1,
∴x12+x22=(x1+x2)2-2x1x2=(2k-1)2-2(k2+k-1)=2k2-6k+3,
∵x12+x22=11,
∴2k2-6k+3=11,解得k=4,或k=-1,
∵k≤![]() ,
,
∴k=4(舍去),
∴k=-1.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.

(1)当t=2时,求线段PQ的长度;
(2)当t为何值时,△PCQ的面积等于5cm2?
(3)在P、Q运动过程中,在某一时刻,若将△PQC翻折,得到△EPQ,如图2,PE与AB能否垂直?若能,求出相应的t值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
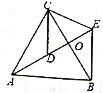
【题目】如图,△ACB和△DCE均为等腰三角形,点A、D、E在同一条直线上,BC和AE相交于点O,连接BE,若∠CAB=∠CBA=∠CDE=∠CED=50°。
(1)求证:AD=BE;
(2)求∠AEB。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=BC,AB=8,点D为AB的中点,若直角MDN绕点D旋转,分别交AC于点E,交BC于F,则下列说法:①AE=CF;②EC+CF=4![]() ;③DE=DF;④若△ECF面积为一个定值,则EF长也是一个定值,其中正确的结论是_____.
;③DE=DF;④若△ECF面积为一个定值,则EF长也是一个定值,其中正确的结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
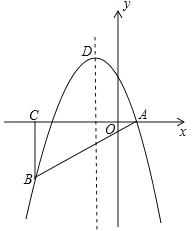
【题目】如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线![]() 经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.
经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.
(1)求抛物线的解析式;
(2)点E是直角三角形ABC斜边AB上的一个动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段FE的长度最大时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点P,使△PEF是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,已知抛物线 y ax![]() bx c 经过 A3,0,B 1,0 ,C 0,3 三点,其顶点为D,对称轴是直线l , l 与 x 轴交于点 H .
bx c 经过 A3,0,B 1,0 ,C 0,3 三点,其顶点为D,对称轴是直线l , l 与 x 轴交于点 H .
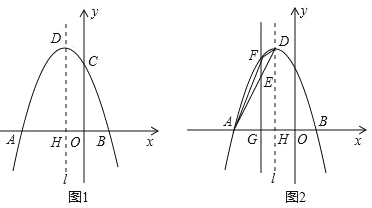
(1)求该抛物线的解析式;
(2)若点 P 是该抛物线对称轴l 上的一个动点,求PBC 周长的最小值;
(3)如图 2,若 E 是线段 AD 上的一个动点( E 与 A, D 不重合),过 E 点作平行于 y 轴的直线交抛物线于点 F ,交 x 轴于点G ,设点 E 的横坐标为m ,四边形 AODF 的面积为 S 。
①求 S 与 m 的函数关系式;
② S 是否存在最大值,若存在,求出最大值及此时点 E 的坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠A=25°,∠B=40°.
(1)求作:⊙O,使⊙O经过A、C两点,且圆心落在AB边上;
(要求:尺规作图,保留作图痕迹,不写作法.)
(2)求证:BC是(1)中所作⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解某市中学生的体能状况,应采用普查的方式
B.“打开电视机,正在播放足球比赛”是必然事件
C.“掷一枚硬币正面朝上的概率是![]() ”表示每抛掷硬币2次就有1次正面朝上
”表示每抛掷硬币2次就有1次正面朝上
D.两运动员10次射击成绩的平均数相同,则方差小的运动员成绩更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
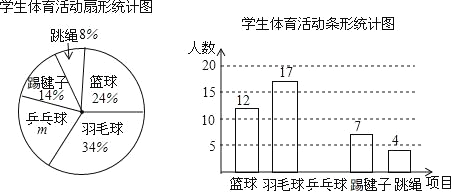
(1)m= %,这次共抽取了 名学生进行调查;并补全条形图;
(2)请你估计该校约有 名学生喜爱打篮球;
(3)现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com