
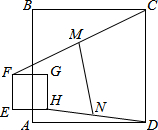
 如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )
如图,边长为2的正方形EFGH在边长为6的正方形ABCD所在平面上移动,始终保持EF∥AB.线段CF的中点为M,DH的中点为N,则线段MN的长为( )| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{17}}{2}$ | C. | $\sqrt{17}$ | D. | $\frac{4}{3}$$\sqrt{10}$ |
分析 连接HM并延长至点P,使MP=MH,作PQ⊥CD于点Q,连接PC、FH、PD,由△FHM≌△CPM,求出PC=FH=$\sqrt{2}$,根据等腰直角三角形的性质求出PQ=CQ=2,再运用勾股定理求出PD,根据三角形中位线性质定理可求出MN的长.
解答 解:连接HM并延长至点P,使MP=MH,作PQ⊥CD于点Q,连接PC、FH、PD,
∵M是线段CF的中点,
∴MF=MC,
在△FHM和△CPM中,
$\left\{\begin{array}{l}{MF=MC}\\{∠FMH=∠CMP}\\{MP=MH}\end{array}\right.$,
∴△FHM≌△CPM,
∴FH=PC,∠HFM=∠PCM,
∵EF=EH=2,
∴FH=PC=2$\sqrt{2}$,
∵FG∥BC,
∴∠GFM=∠BCM,
∴∠HFG=∠PCB=45°,
∴∠PCQ=45°,
∴PQ=QC=2,
∴DQ=CD+CQ=8,
∴PD=2$\sqrt{17}$,
∵线段HP的中点为M,DH的中点为N,
∴MN=$\frac{1}{2}$PD=$\sqrt{17}$.
故选:C.
点评 本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质、勾股定理以及三角形中位线性质定理的综合运用,通过辅助线构造全等三角形和三角形中位线是解决问题的关键.


科目:初中数学 来源: 题型:解答题
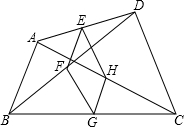 如图,四边形ABCD中,E、F、G、H分别为AD、BD、BC、AC的中点,顺次连结点E、F、G、H,所得四边形是一个怎样的四边形?请说明理由;若四边形EFGH是一个菱形,则四边形ABCD应满足什么条件?
如图,四边形ABCD中,E、F、G、H分别为AD、BD、BC、AC的中点,顺次连结点E、F、G、H,所得四边形是一个怎样的四边形?请说明理由;若四边形EFGH是一个菱形,则四边形ABCD应满足什么条件?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
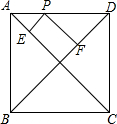 如图,在正方形ABCD中,P是AD上任一点,PE⊥AC,PF⊥BD,点E、F分别是垂足,AC=10,则PE+PF的值是( )
如图,在正方形ABCD中,P是AD上任一点,PE⊥AC,PF⊥BD,点E、F分别是垂足,AC=10,则PE+PF的值是( )| A. | 10 | B. | 5 | C. | 20 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
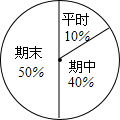 小军八年级上学期的数学成绩如表所示:易知小军上学期平时的平均成绩105分.
小军八年级上学期的数学成绩如表所示:易知小军上学期平时的平均成绩105分.| 测验类别 | 平时 | 期中考试 | 期末考试 | |||
| 测验1 | 测验2 | 测验3 | 测验4 | |||
| 成绩 | 110 | 105 | 95 | 110 | 108 | 112 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com