△ABC的周长为30 cm，把△ABC的边AC对折，使顶点C和点A重合，折痕交BC边于点D，交AC边于点E，连接AD，若AE＝4 cm，则△ABD的周长是
A．22 cm B．20 cm C．18 cm D．15 cm
名校课堂系列答案科目：初中数学 来源： 题型：
如图，在四边形ABCD中，∠BAD=∠BCD=90°，BC=6，CD=AC=8，M、N分别是对角线BD、AC的中点．
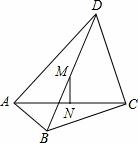
（1）求证：MN⊥AC．
（2）求MN的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
某公交公司的公共汽车和出租车每天从沂源出发往返于沂源和济南两地，出租车比公共汽车多往返一趟，如图表示出租车距沂源的路程
（单位：千米）与所用时间
（单位：小时）的函数图象．已知公共汽车比出租车晚1小时出发，到达济南后休息2小时，然后按原路原速返回，结果比出租车最后一次返回沂源早1小时．
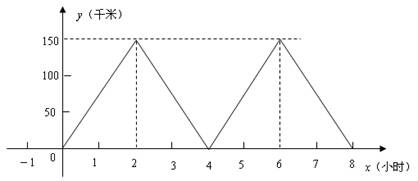
（1）请在图中画出公共汽车距沂源的路程（千米）与所用时间（小时）的函数图象；
（2）求两车在途中相遇的次数（直接写出答案）；
（3）求两车最后一次相遇时，距沂源的路程．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，正方形ABCD和正方形AEFG有公共的顶点A，连BG、DE，M为DE的中点，连AM.
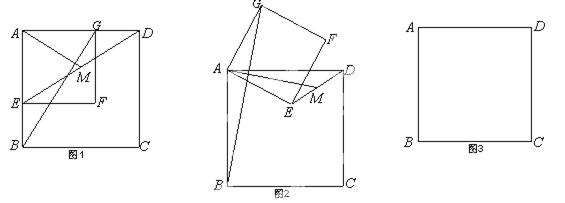
（1）如图1，AE、AG分别与AB、AD重合时，AM和BG的大小和位置关系分别是 、_ ____；
（2）将图1中的正方形AEFG绕A点旋转到如图2，则（1）中的结论是否仍成立？试证明你的结论；
（3）若将图1中的正方形AEFG绕A点逆时针旋转到正方形ABCD外时，则AM和BG的大小和位置关系分别是__________、____________，请你在图3中画出图形，并直
接写出结论，不要求证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（ ）
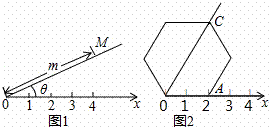
A．（60°，4） B．（45°，4） C．（60°，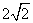
） D．（50°，）
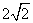查看答案和解析>>
科目：初中数学 来源： 题型：
已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．
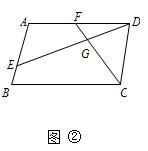
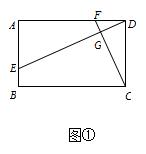
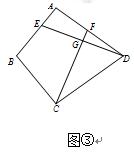
（1）如图①，若四边形ABCD是矩形，且DE⊥CF，求证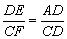
；
（2）如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，使得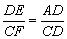成立？并证明你的结论；
（3）如图③，若BA=BC=2，DA=DC=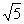
，∠BAD＝90°，DE⊥CF，试求
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
与⊙O在第一象限内交于P、Q 两点，分别过P、Q两点向x轴和y轴作垂线，已知点P坐标为（1，3），则图中阴影部分的面积为 ．
，则函数
和
的图象大致是【 】
B. 
C. 
D. 