
【题目】仔细阅读下面倒题.解答问题:
例题:已知二次三项式,x2-4x+m分解因式后有一个因式是(x+3).求另一个因式以及m的值.
解:方法一:设另一个因式为(x+n),得x2-4x+m=(x+3)(x+n).则x2-4x+m=x2+(n+3)x+3n,∴ ![]() ,解得
,解得 ![]() ,∴另一个因式为(x-7),m的值为-21.
,∴另一个因式为(x-7),m的值为-21.
方法二:设x2-4x+m=k(x+3)(k≠0),当x=-3时,左边-9+12+m,右边=0,∴9+12+m=0,解得m=-21,将x2-4x-21分解因式,得另一个因式为(x-7).
仿照以上方法一或方法二解答:已知二次三项式8x2-14x-a分解因式后有一个因式是(2x-3).求另一个因式以及a的值.
【答案】解:参照方法一解答:∵二次项系数为8,一个因式(2x-3)的一次项系数是2,则另一个因式的一次项系数为8÷2=4,则可设另一个因式为(4x+b),
得8x2-14x-a=(2x-3)(4x+b)=8x2+(2b-12)x-3b,
∴ ![]() ,解得
,解得 ![]() ,
,
则另一个因式为(4x-1),a=-3.
参照方法二解答:设8x2-14x-a=k(2x-3) (k≠0),当x= ![]() 时,左边=18-21-a,右边=0,则18-21-a=0,解得a=-3.
时,左边=18-21-a,右边=0,则18-21-a=0,解得a=-3.
则另一个因式为(4x-1).
【解析】根据因式分解的定义可知,等号两边只是形式不一样,但结果相等.
【考点精析】根据题目的已知条件,利用因式分解的定义的相关知识可以得到问题的答案,需要掌握因式分解的最后结果必须是几个整式的乘积,否则不是因式分解;因式分解的结果必须进行到每个因式在有理数范围内不能再分解为止.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,有足够多的边长为a的小正方形(A类)、宽为a长为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料若干可以拼出一些长方形来解释某些等式.
尝试解决:
(1)取图①中的若干个(三类图形都要取到)拼成一个长方形,使其面积为(a+b)(a+b),在下面虚线框中画出图形,并根据图形回答(a+b)(a+b)= .
(2)图②是由图①中的三种材料拼出的一个长方形,根据②可以得到并解释等式:
(3)若取其中的若干个(三类图形都要取到)拼成一个长方形,使其面积为3a2+4ab+b2 . 你画的图中需要B类卡片张;
(4)分解因式:3a2+4ab+b2 .
拓展研究:如图③,大正方形的边长为m,小正方形的边长为n,若用m、n表示四个直角三角形的两直角边边长(b>a),观察图案,以下关系式中正确的有 . (填写正确选项的序号)
(1)ab= ![]()
(2)a+b=m
(3)a2+b2= ![]()
(4)a2+b2=m2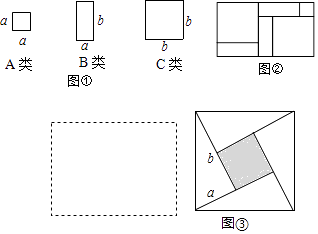
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C′,BC′与AD交于点E,若AB=3,BC=4,则DE的长为 . 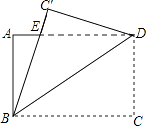
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程mx2﹣3(m﹣1)x+2m﹣3=0(m>3).
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x1 , x2(用含m的代数式表示);
①求方程的两个实数根x1 , x2(用含m的代数式表示);
②若mx1<8﹣4x2 , 直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地2018年农民人均年收入为49000元,计划到2020年,农民人均年收入达到90000元,设人均年收入的平均增长率为x,则可列方程_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,射线AB∥CD,∠CAB的角平分线交射线CD于点P1 . 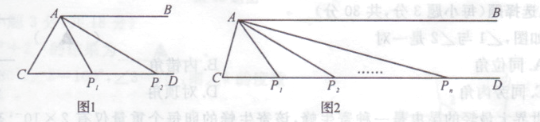
(1)若∠C=50°,求∠AP1C的度数.
(2)如图1,作∠P1AB的角平分线交射线CD于点P2 . 猜想∠AP1C与∠AP2C的数量关系,并说明理由.
(3)如图2,在(2)的条件下,依次作出∠P2AB的角平分线AP3 . ∠P3AB的角平分线AP4 , ……“∠Pn-1AB的角平分线APn . 其中点P3,P4…,Pn-1Pn都在射线CD上,若∠APnC=x,直接写出∠C的度数(用含x的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知北京位于东经116.4°,北纬39.9°,如果规定“经度在前,纬度在后”,那么我们可以用有序数对________表示北京的位置;仿照此表示方法,某地的地理位置用有序数对(119°,19.9°)表示,则其地理位置位于东经________°,北纬________°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com