
ЎѕМвДїЎїИзНјЈ¬УРЧг№»¶аµД±Яі¤ОЄaµДРЎХэ·ЅРОЈЁAАаЈ©ЎўїнОЄaі¤ОЄbµДі¤·ЅРОЈЁBАаЈ©ТФј°±Яі¤ОЄbµДґуХэ·ЅРОЈЁCАаЈ©Ј¬·ўПЦАыУГНјўЩЦРµДИэЦЦІДБПИфёЙїЙТФЖґіцТ»Р©і¤·ЅРОАґЅвКНДіР©µИКЅЈ®
іўКФЅвѕцЈє
ЈЁ1Ј©ИЎНјўЩЦРµДИфёЙёцЈЁИэАаНјРО¶јТЄИЎµЅЈ©ЖґіЙТ»ёці¤·ЅРОЈ¬К№ЖдГж»эОЄЈЁa+bЈ©ЈЁa+bЈ©Ј¬ФЪПВГжРйПЯїтЦР»іцНјРОЈ¬ІўёщѕЭНјРО»ШґрЈЁa+bЈ©ЈЁa+bЈ©= Ј®
ЈЁ2Ј©НјўЪКЗУЙНјўЩЦРµДИэЦЦІДБПЖґіцµДТ»ёці¤·ЅРОЈ¬ёщѕЭўЪїЙТФµГµЅІўЅвКНµИКЅЈє
ЈЁ3Ј©ИфИЎЖдЦРµДИфёЙёцЈЁИэАаНјРО¶јТЄИЎµЅЈ©ЖґіЙТ»ёці¤·ЅРОЈ¬К№ЖдГж»эОЄ3a2+4ab+b2 Ј® Дг»µДНјЦРРиТЄBАаїЁЖ¬ХЕЈ»
ЈЁ4Ј©·ЦЅвТтКЅЈє3a2+4ab+b2 Ј®
НШХ№СРѕїЈєИзНјўЫЈ¬ґуХэ·ЅРОµД±Яі¤ОЄmЈ¬РЎХэ·ЅРОµД±Яі¤ОЄnЈ¬ИфУГmЎўn±нКѕЛДёцЦ±ЅЗИэЅЗРОµДБЅЦ±ЅЗ±Я±Яі¤ЈЁbЈѕaЈ©Ј¬№ЫІмНј°ёЈ¬ТФПВ№ШПµКЅЦРХэИ·µДУР Ј® ЈЁМоРґХэИ·СЎПоµДРтєЕЈ©
ЈЁ1Ј©ab= ![]()
ЈЁ2Ј©a+b=m
ЈЁ3Ј©a2+b2= ![]()
ЈЁ4Ј©a2+b2=m2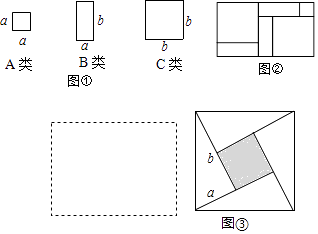
Ўѕґр°ёЎї
ЈЁ1Ј©a2+2ab+b2
ЈЁ2Ј©a2+3ab+2b2
ЈЁ3Ј©4
ЈЁ4Ј©ЈЁ1Ј©Ј¬ЈЁ4Ј©
ЎѕЅвОцЎїЅвЈєЈЁ1Ј©ИзНјЈє
ЈЁa+bЈ©ЈЁa+bЈ©=a2+2ab+b2 Ј®
ЛщТФґр°ёКЗЈєa2+2ab+b2Ј»ЈЁ2Ј©і¤·ЅРОµДГж»эОЄa2+3ab+2b2 Ј¬
ЛщТФґр°ёКЗЈєa2+3ab+2b2 Ј® ЈЁ3Ј©ЎЯ3a2+4ab+b2=ЈЁ3a+bЈ©ЈЁa+bЈ©Ј¬
ЎаРиТЄBАаїЁЖ¬4ХЕЈ»
ЛщТФґр°ёКЗЈє4Ј»ЈЁ4Ј©ЅвЈєёщѕЭНјўЫµГЈє4ЎБ ![]() ab+n2=m2 Ј¬
ab+n2=m2 Ј¬
Ўаab= ![]() Ј¬
Ј¬
ЎЯЈЁb©ЃaЈ©2=n2 Ј¬ 4ЎБ ![]() ab+n2=2ab+ЈЁb©ЃaЈ©2=m2 Ј¬
ab+n2=2ab+ЈЁb©ЃaЈ©2=m2 Ј¬
Ўаa2+b2=m2 Ј¬
ЎаЈЁ1Ј©Ј¬ЈЁ4Ј©ХэИ·Ј¬
ЛщТФґр°ёКЗЈєЈЁ1Ј©Ј¬ЈЁ4Ј©Ј®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЎчABCЦРЈ¬ЎПA=60ЎгЈ¬BDЎўCD·Ц±рЖЅ·ЦЎПABCЎўЎПACBЈ¬MЎўNЎўQ·Ц±рФЪDBЎўDCЎўBCµДСУі¤ПЯЙПЈ¬BEЎўCE·Ц±рЖЅ·ЦЎПMBCЎўЎПBCNЈ¬BFЎўCF·Ц±рЖЅ·ЦЎПEBCЎўЎПECQЈ¬ФтЎПF= Ј® 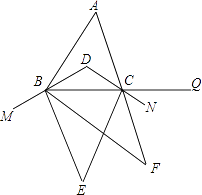
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБРєЇКэЦРЈ¬yЛжxµДФцґу¶шјхРЎµДєЇКэКЗЈЁ Ј©
A.y=2x+8
B.y=©Ѓ2+4x
C.y=©Ѓ2x+8
D.y=4x
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЦ±ПЯMNУлЦ±ПЯPQґ№Ц±ПаЅ»УЪOЈ¬µгAФЪЦ±ПЯPQЙПФЛ¶ЇЈ¬µгBФЪЦ±ПЯMNЙПФЛ¶ЇЈ® 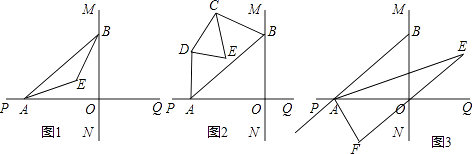
ЈЁ1Ј©ИзНј1Ј¬ТСЦЄAEЎўBE·Ц±рКЗЎПBAOєНЎПABOЅЗµДЖЅ·ЦПЯЈ¬µгAЎўBФЪФЛ¶ЇµД№эіМЦРЈ¬ЎПAEBµДґуРЎКЗ·с»б·ўЙъ±д»ЇЈїИф·ўЙъ±д»ЇЈ¬ЗлЛµГч±д»ЇµДЗйїцЈ»ИфІ»·ўЙъ±д»ЇЈ¬КФЗуіцЎПAEBµДґуРЎЈ®
ЈЁ2Ј©ИзНј2Ј¬ТСЦЄABІ»ЖЅРРCDЈ¬ADЎўBC·Ц±рКЗЎПBAPєНЎПABMµДЅЗЖЅ·ЦПЯЈ¬УЦDEЎўCE·Ц±рКЗЎПADCєНЎПBCDµДЅЗЖЅ·ЦПЯЈ¬µгAЎўBФЪФЛ¶ЇµД№эіМЦРЈ¬ЎПCEDµДґуРЎКЗ·с»б·ўЙъ±д»ЇЈїИф·ўЙъ±д»ЇЈ¬ЗлЛµГчАнУЙЈ»ИфІ»·ўЙъ±д»ЇЈ¬КФЗуіцЖдЦµЈ®
ЈЁ3Ј©ИзНј3Ј¬СУі¤BAЦБGЈ¬ТСЦЄЎПBAOЎўЎПOAGµДЅЗЖЅ·ЦПЯУлЎПBOQµДЅЗЖЅ·ЦПЯј°СУі¤ПЯПаЅ»УЪEЎўFЈ¬ФЪЎчAEFЦРЈ¬Из№ыУРТ»ёцЅЗКЗБнТ»ёцЅЗµД3±¶Ј¬КФЗуЎПABOµД¶ИКэЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБР¶аПоКЅЦРЈ¬ДЬУГМбИЎ№«ТтКЅ·Ё·ЦЅвТтКЅµДКЗЈЁ Ј©
A.x2©Ѓy
B.x2+2x
C.x2+y2
D.x2©Ѓxy+y2
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБРФЛЛгµДЅб№ыОЄa6µДКЗЈЁ Ј©
A.a3+a3
B.ЈЁa3Ј©3
C.a3a3
D.a12ЎВa2
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЛДМхЦ±ПЯБЅБЅПаЅ»Ј¬ЗТИОТвИэМхІ»ПаЅ»УЪН¬Т»µгЈ¬ФтЛДМхЦ±ПЯ№ІїЙ№№іЙµДН¬О»ЅЗУРЧй
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИфєЇКэy=mx2+2x+1µДНјПуУлxЦбЦ»УРТ»ёц№«№ІµгЈ¬ФтіЈКэmµДЦµКЗ Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЧРПёФД¶БПВГжµ№МвЈ®ЅвґрОКМвЈє
АэМвЈєТСЦЄ¶юґОИэПоКЅЈ¬x2-4x+m·ЦЅвТтКЅєуУРТ»ёцТтКЅКЗ(x+3)Ј®ЗуБнТ»ёцТтКЅТФј°mµДЦµЈ®
ЅвЈє·Ѕ·ЁТ»ЈєЙиБнТ»ёцТтКЅОЄ(x+n)Ј¬µГx2-4x+m=(x+3)(x+n)Ј®Фтx2-4x+m=x2+(n+3)x+3nЈ¬Ўа ![]() Ј¬ЅвµГ
Ј¬ЅвµГ ![]() Ј¬ЎаБнТ»ёцТтКЅОЄ(x-7)Ј¬mµДЦµОЄ-21.
Ј¬ЎаБнТ»ёцТтКЅОЄ(x-7)Ј¬mµДЦµОЄ-21.
·Ѕ·Ё¶юЈєЙиx2-4x+m=k(x+3)(kЎЩ0)Ј¬µ±x=-3К±Ј¬Чу±Я-9+12+mЈ¬УТ±Я=0Ј¬Ўа9+12+m=0Ј¬ЅвµГm=-21Ј¬Ѕ«x2-4x-21·ЦЅвТтКЅЈ¬µГБнТ»ёцТтКЅОЄ(x-7).
·ВХХТФЙП·Ѕ·ЁТ»»т·Ѕ·Ё¶юЅвґрЈєТСЦЄ¶юґОИэПоКЅ8x2-14x-a·ЦЅвТтКЅєуУРТ»ёцТтКЅКЗ(2x-3)Ј®ЗуБнТ»ёцТтКЅТФј°aµДЦµЈ®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com