
����Ŀ���α�����һ�����⣺
��һ��������״��ͼ1���ϲ���һ����Բ���²���һ�����Σ������������IJ����ܳ�Ϊ6m�����������������ʹ��������
�������Ĵ��ǣ���������Բ�İ뾶ԼΪ0.35mʱ����������ֵԼΪ1.05m2��
��������ı������������״���ϲ���Ϊ��������������ɵľ��Σ���ͼ2�������ܳ���Ϊ6m������ͼ3������������⣺

��1����ABΪ1m�����ʱ�������������
��2����α��е�����Ƚϣ��ı䴰����״��������������ֵ��û�б����ͨ������˵����
���𰸡���1��![]() ����2�����ֵΪ
����2�����ֵΪ![]() ����������������ֵ�����.
����������������ֵ�����.
��������
��1�����ݾ��κ������ε��ܳ����н�ɣ�
��2����ABΪxcm�����ö��κ�������ֵ��ɣ�
��1������֪�ɵã�AD=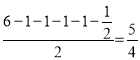 ��S=1��
��S=1��![]() m2��
m2��
��2����AB=xm����AD=3��![]() xm�� ��3-
xm�� ��3-![]() x
x![]() 0 ��
0 ��![]() ��
��
�贰�����ΪS������֪�ã�S=AB��AD=x��3-![]() x��=
x��=![]()
��x=![]() mʱ����x=
mʱ����x=![]() m��
m��![]() �ķ�Χ�ڣ�S���ֵ=
�ķ�Χ�ڣ�S���ֵ=![]() ��
��
����α��е�����Ƚϣ����ڴ�������������ֵ���


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P��G������ABCD�ı�BC��DC���е㣬K�����εĶԽ���BD�ϵĶ��㣬��BD��8��AC��6����KP+KG����Сֵ��_____��
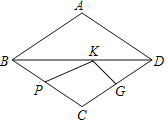
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017����ʡ��ˮ�У���ABC�͡�DEF������ȫ�ȵĵ���ֱ�������Σ���BAC=��EDF=90�㣬��DEF�Ķ���E���ABC��б��BC���е��غϣ�����DEF�Ƶ�E��ת����ת�����У��߶�DE���߶�AB�ཻ�ڵ�P���߶�EF������CA�ཻ�ڵ�Q��
��1����ͼ�٣�����Q���߶�AC�ϣ���AP=AQʱ����֤����BPE�ա�CQE��
��2����ͼ�ڣ�����Q���߶�CA���ӳ�����ʱ����֤����BPE�ס�CEQ������BP=2��CQ=9ʱBC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD�ı߳�Ϊ12��E�DZ�CD��һ�㣬����AE���۵���ֽƬ��ʹ��A����AE�ϵ�G�㣬��ʹ�ۺ۾�����B���õ��ۺ�BF����F��AD�ϣ���DE=5����GE��Ϊ_______________.
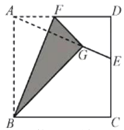
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c(a��0)�ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ(3��0)���䲿��ͼ����ͼ��ʾ�����н��ۣ�
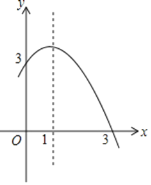
��4ac<b2��
�ڷ���ax2+bx+c=0����������x1=-2 x2=3��
��3a+c=0��
�ܵ�y>0ʱ��x��ȡֵ��Χ��-1<x<3��
�ݵ�x<0ʱ��y��x���������
���н�����ȷ�ĸ�����( )
A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��E��F�ֱ�ΪBC��AC��AB���е㣬AD��BE��CF�ཻ�ڵ�O��AB��6��AC��8��BC��10����DE��_____��OA��_____��OF��_____����DEF����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�Ǿ���ABCD�ı���һ���㣬�������߳�AB��BC���ֱ�Ϊ15��20����ôP�����������Խ���AC��BD�ľ���֮���ǣ�������
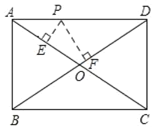
A.6B.12C.24D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
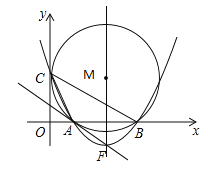
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���M�������ǣ�5��4������M��y�������ڵ�C����x���ཻ��A��B���㣮
��1�����A��B��C������ֱ���A��__��__����B��__��__����C��__��__����
��2���辭��A��B����������߽���ʽΪ![]() �����Ķ���ΪF����֤��ֱ��FA���M���У�
�����Ķ���ΪF����֤��ֱ��FA���M���У�
��3���������ߵĶԳ����ϣ��Ƿ���ڵ�P���ҵ�P��x����Ϸ���ʹ��PBC�ǵ��������Σ�������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
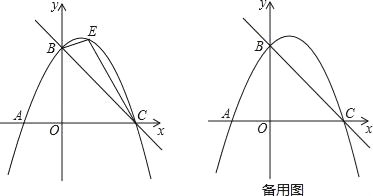
����Ŀ����ͼ��ֱ��y=��![]() x+4��x�ύ�ڵ�C����y�ύ�ڵ�B��������y=ax2+
x+4��x�ύ�ڵ�C����y�ύ�ڵ�B��������y=ax2+![]() x+c����B��C���㣮
x+c����B��C���㣮
��1���������ߵĽ���ʽ��
��2����ͼ����E��ֱ��BC�Ϸ��������ϵ�һ���㣬����BEC������ʱ���������E�����ꣻ
��3���ڣ�2���Ľ����£�����E��y���ƽ���߽�ֱ��BC�ڵ�M������AM����Q�������߶Գ����ϵĶ��㣬�����������Ƿ���ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com