
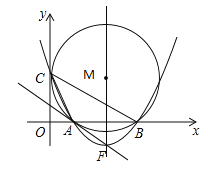
【题目】如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A、B两点.
(1)则点A、B、C的坐标分别是A(__,__),B(__,__),C(__,__);
(2)设经过A、B两点的抛物线解析式为![]() ,它的顶点为F,求证:直线FA与⊙M相切;
,它的顶点为F,求证:直线FA与⊙M相切;
(3)在抛物线的对称轴上,是否存在点P,且点P在x轴的上方,使△PBC是等腰三角形.如果存在,请求出点P的坐标;如果不存在,请说明理由.
【答案】(1)A(2,0),B(8,0),C(0,4);(2)证明见试题解析;(3)P(5,4),或(5,![]() ),或(5,
),或(5,![]() ).
).
【解析】
(1)连接MC,则MC垂直于y轴,MA=MC=5,MD=4,由勾股定理可计算AD和DB;
(2)把A、或B或C的坐标代入y=![]() ,确定二次函数表达式y=
,确定二次函数表达式y=![]() ,连接MA,根据勾股定理计算AF,由勾股定理逆定理判断MA⊥AF,从而说明FA是切线;
,连接MA,根据勾股定理计算AF,由勾股定理逆定理判断MA⊥AF,从而说明FA是切线;
(3)设P(x,4),当C为顶点时,在Rt△CMP1中用x表示CP1,根据![]() 列方程求解;当B为顶点时,在Rt△BDP2中用x表示CP2,根据
列方程求解;当B为顶点时,在Rt△BDP2中用x表示CP2,根据![]() 列方程求解;当P是顶点时,易知P和M重合.
列方程求解;当P是顶点时,易知P和M重合.
解:(1)连接MC,则MC垂直于y轴,MA=MC=5,MD=4,在Rt△AMD中,AD=![]() =3,同理在Rt△BMD中,BD=3
=3,同理在Rt△BMD中,BD=3
∴A(2,0),B(8,0),C(0,4);
(2)把A(2,0)y=![]() ,解得k=-
,解得k=-![]()
∴y=![]() ,∴F(5,-
,∴F(5,-![]() )
)
连接MA,则MF=4+![]() =
=![]() ,AF=
,AF=![]() =
=![]()
∴![]()
∴MA⊥AF
∴FA与⊙M相切;
(3)设P(x,4),![]()
当C为顶点时,在Rt△CMP1中,![]()
∴![]() ,x=
,x=![]()
点P在x轴上方,故x=![]() ,所以(
,所以(![]() ,4);
,4);
当B为顶点时,在Rt△BDP2中,![]()
∴![]() ,x=
,x=![]() ,点P在x轴上方
,点P在x轴上方
故x=![]() ,所以(
,所以(![]() ,4);
,4);
当P是顶点时,P和M重合,P3(5,4).
综上当P(![]() ,4)、(
,4)、(![]() ,4)或(5,4)时△PBC是等腰三角形.
,4)或(5,4)时△PBC是等腰三角形.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点P在AB边上(不含端点A,B),以PC为直径作圆.圆与BC,CA分别相交于点M,N,则线段MN长度的最小值为________.
,动点P在AB边上(不含端点A,B),以PC为直径作圆.圆与BC,CA分别相交于点M,N,则线段MN长度的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2.
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:

(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
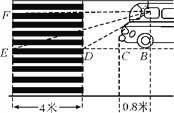
【题目】如图,某小学门口有一直线马路,交警在门口设有一条宽度为4米的斑马线,为安全起见,规定车头距斑马线后端的水平距离不得低于2米,现有一旅游车在路口遇红灯刹车停下,汽车里司机与斑马线前后两端的视角分别为∠FAE=15°和∠FAD=30°,司机距车头的水平距离为0.8米,试问该旅游车停车是否符合上述安全标准?(E,D,C,B四点在平行于斑马线的同一直线上)(参考数据:tan15°=2-![]() ,
,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象过点(1,![]() )、(2,4)、(﹣1,
)、(2,4)、(﹣1,![]() )与x轴分别交于B(左)、C两点,与y轴交于点A.
)与x轴分别交于B(左)、C两点,与y轴交于点A.
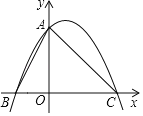
(1)求二次函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向.
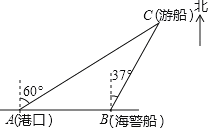
(1)求海警船距离事故船C的距离BC.
(2)若海警船以40海里/小时的速度前往救援,求海警船到达事故船C处大约所需的时间.(温馨提示:sin 53°≈0.8,cos 53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
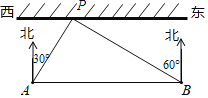
【题目】为了保证端午节龙舟赛在我市侨港海域顺利举办,某部门工作人员乘快艇到侨港海域考察水情,以每秒11米的速度沿平行于岸边的赛道AB由西向东行驶,在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
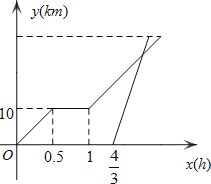
【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com