
定义:数学活动课上,乐老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
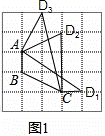
理解:(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;
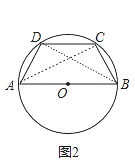
(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.求证:四边形ABCD是对等四边形;
(3)如图3,在Rt△PBC中,∠PCB=90°,BC=11,tan∠PBC=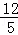 ,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D
,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D ,使四边形ABCD为对等四边形,并求出CD的长.
,使四边形ABCD为对等四边形,并求出CD的长.

解:(1)如图1所示(画2个即可).
(2)如图2,连接AC,BD,
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
在Rt△ADB和Rt△ACB中,
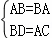
∴Rt△ADB≌Rt△ACB,
∴AD=BC,
又∵AB是⊙O的直径,
∴AB≠CD,
∴四边形ABCD是对等四边形.
(3)如图3,点D的位置如图所示:
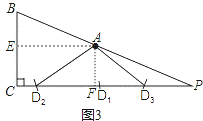
①若CD=AB,此时点D在D1的位置,CD1=AB=13;
②若AD=BC=11,此时点D在D2、D3的位置,AD2=AD3=BC=11,
过点A分别作AE⊥BC,AF⊥PC,垂足为E,F,
设BE=x,
∵tan∠PBC= ,
,
∴AE= ,
,
在Rt△ABE中,AE2+BE2=AB2,
即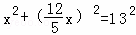 ,
,
解得:x1=5,x2﹣5(舍去),
∴BE=5,AE=12,
∴CE=BC﹣BE=6,
由四边形AECF为矩形,可得AF=CE=6,CF=AE=12,
在Rt△AFD2中,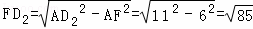 ,
,
∴ ,
, ,
,
综上所述,CD的长度为13、12﹣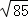 或12+
或12+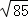 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
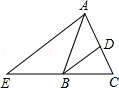
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )
|
| A. | 40° | B. | 45° | C. | 60° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:
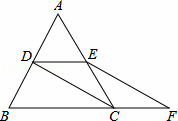
如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=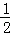 BC,连接CD和EF.
BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
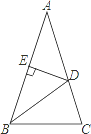
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
某市测得一周PM2.5的日均值(单位:微克/立方米)如下:31,30,34,35,36,34,31,对这组数据下列说法正确的是( )
|
| A. | 众数是35 | B. | 中位数是34 | C. | 平均数是35 | D. | 方差是6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列各式及其展开式:
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
…
请你猜想(a+b)10的展开式第三项的系数是( )
|
| A. | 36 | B. | 45 | C. | 55 | D. | 66 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
(1)求证:AE=DF.
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
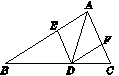
第21题图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com