
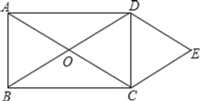
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE//AC,CE//BD,DE、CE相交于点E.
求证:(1)四边形OCED是菱形.
(2)连接OE,若AD=5,CD=3,求菱形OCED的面积.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
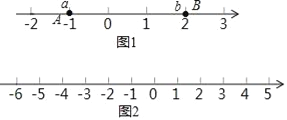
如图1,在数轴上A点衰示的数为a,B点表示的数为b,则点A到点B的距离记为AB.线段AB的长可以用右边的数减去左边的数表示,即AB﹣b﹣a.
请用上面的知识解答下面的问题:
如图2,一个点从数轴上的原点开始,先向左移动1cm到达A点,再向左移动2cm到达B点,然后向右移动7cm到达C点,用1个单位长度表示1cm.
(1)请你在数轴上表示出A.B.C三点的位置:
(2)点C到点人的距离CA= cm;若数轴上有一点D,且AD=4,则点D表示的数为 ;
(3)若将点A向右移动xcm,则移动后的点表示的数为 ;(用代数式表示)
(4)若点B以每秒2cm的速度向左移动,同时A.C点分别以每秒1cm、4cm的速度向右移动.设移动时间为t秒,
试探索:CA﹣AB的值是否会随着t的变化而改变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
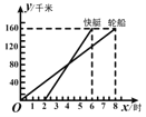
【题目】如图所示,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程y(千米)随时间t(时)变化的图象,根据图象回答下列问题
(1)轮船的行驶速度是___________km/h;
(2)当2≤t≤6时,求快艇行驶过程y与t的函数关系式;
(3)当快艇与乙港相距40 km时,快艇和轮船相距___________km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校七年级某班准备买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副![]() 元,乒乓球每盒
元,乒乓球每盒![]() 元,经商谈后,甲商店每买一副乒乓球拍赠一盒乒乓球,乙商店全部按定价的
元,经商谈后,甲商店每买一副乒乓球拍赠一盒乒乓球,乙商店全部按定价的![]() 折优惠这个班级需要球拍
折优惠这个班级需要球拍![]() 副,乒乓球
副,乒乓球![]() 盒(
盒(![]() ).
).
(1)分别求甲、乙两家商店购买这些商品所箭的费用(用含x的代数式表示);
(2)当![]() 时,购买所需商品去哪家商店合算?请通过计算说明理由.
时,购买所需商品去哪家商店合算?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
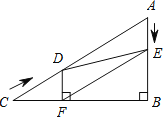
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,若一个点到一条直线的距离不大于1,则 称这个点是该直线的“邻点”.在平面直角坐标系中,已知点![]()
![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() 平行于
平行于![]() 轴,并将
轴,并将![]() 进行平移,平移后点
进行平移,平移后点![]() 分别对应点
分别对应点![]() .
.
(1)点![]() (填写是或不是)直线
(填写是或不是)直线![]() 的“邻点”,请说明理由;
的“邻点”,请说明理由;
(2)若点![]() 刚好落在直线
刚好落在直线![]() 上,点
上,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 落在
落在![]() 轴上,且
轴上,且![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标,判断点
的坐标,判断点![]() 是否是直线
是否是直线![]() 的“邻点”,并说明理由.
的“邻点”,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象过点A(0,3)和点B(3,0),且与正比例函数
的图象过点A(0,3)和点B(3,0),且与正比例函数![]() 的图象交于点P.
的图象交于点P.

(1)求函数![]() 的解析式和点P的坐标.
的解析式和点P的坐标.
(2)画出两个函数 的图象,并直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
(3)若点Q是![]() 轴上一点,且△PQB的面积为8,求点Q的坐标.
轴上一点,且△PQB的面积为8,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com