
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.

(1)、如图a,求证:△BCP≌△DCQ;
(2)、如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
【答案】(1)证明见试题解析;(2)①证明见试题解析;②△DEP为等腰直角三角形.
【解析】试题分析:(1)、根据正方形性质得出BC=DC,根据旋转图形的性质得出CP=CQ以及∠PCB=∠QCD,从而得出三角形全等;(2)、①、根据全等得出∠PBC=∠QBC,设BE和CD交点为M,根据对顶角得出∠DME=∠BMC,从而说明BE⊥QD;②、根据等边三角形的性质得出PB=PC=BC,∠PBC=∠BPC=∠PCB=60°,则∠PCD=30°,根据BC=DC,CP=CQ得出△PCD为等腰三角形,然后根据△DCQ为等边三角形,从而得出∠DEP=90°,从而得出答案.
试题解析:(1)、∵四边形ABCD是正方形,∴BC=DC
又∵将线段CP绕点C顺时针旋90°得到线段CQ,∴CP=CQ,∠PCQ=90°∴∠PCD+∠QCD=90°
又∵∠PCB+∠PCD=90° ∴∠PCB=∠QCD
在△BCP和△DCQ中 BC=DC,CP=CQ,∠PCB=∠QCD ∴△BCP≌△DCQ
(2)、①∵△BCP≌△DCQ ∴∠PBC=∠QBC
设BE和CD交点为M ∴∠DME=∠BMC ∠MED=∠MCB=90°∴BE⊥QD
②△DEP为等腰直角三角形,
∵△BOP为等边三角形 ∴PB=PC=BC ∠PBC=∠BPC=∠PCB=60°
∴∠PCD=90°-60°=30°∴∠DCQ=90°-60°=30°
又∵BC=DC CP=CQ∴PC=DC DC=CQ ∴△PCD是等腰三角形
△DCQ是等边三角形 ∴∠CPD=∠CDP=75°∠CDQ=60°∴∠EPD=180°-15°-60°=45°
∠EDP=180°-75°-60°="45" °∴∠EPD=∠EDP PE=DE ∴∠DEP=180°-45°-45°=90°
∴△DEP是等腰直角三形


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:

①![]() ;② 方程
;② 方程![]() 的两个根是
的两个根是![]() ;③
;③ ![]() ;④当
;④当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ;⑤ 当
;⑤ 当![]() 时,
时, ![]() 随
随![]() 增大而增大;其中结论正确有____.
增大而增大;其中结论正确有____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:因为一个非负数的绝对值等于它本身,负数的绝对值等于它的相反数,所以当a≥0时|a|=a,当a<0时|a|=﹣a,根据以上阅读完成:
(1)|3.14﹣π|= .
(2)计算:| ![]() ﹣1|+|
﹣1|+| ![]() ﹣
﹣ ![]() |+|
|+| ![]() ﹣
﹣ ![]() |…+|
|…+| ![]() ﹣
﹣ ![]() |+|
|+| ![]() +
+ ![]() |.
|.
查看答案和解析>>
科目:初中数学 来源: 题型:
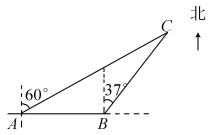
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3, ![]() 的长为π.
的长为π.
(1)直线CD与⊙O相切吗?说明理由。
(2)求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD. 
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com