
【题目】如图,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且AE+AF=AB,

(1)求证:DE⊥DF;
(2)若AC=2,求四边形DEAF的面积.
【答案】(1)见解析;(2)1
【解析】
(1)连接AD,根据等腰直角三角形的性质可得AD=CD,AD⊥BC,∠C=∠B=∠BAD=∠DAC=45°,根据AE+AF=AB,AF+FC=AC可得AE=FC,利用“SAS”证明△DEA≌△DFC,得到∠EDA=∠FDC,利用等量代换即可证得∠EDF=90°,即可得证;
(2)根据全等可知S四边形DEAF=S△ADC,利用勾股定理可求得AD、DC的长,再求△ADC的面积即可完成.
(1)如图,
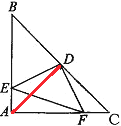
证明:连接AD
∵△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,
∴AD=CD,AD⊥BC,∠C=∠B=∠BAD=∠DAC=45°
∵AE+AF=AB,AF+FC=AC
∴AE=FC
在△DEA和△DFC中
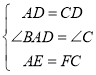
∴△DEA≌△DFC(SAS)
∴∠EDA=∠FDC
∵∠FDC+∠ADF=90°
∴∠EDA+∠ADF=90°
即∠EDF=90°
∴DE⊥DF
(2)

解:∵△DEA≌△DFC
∴S四边形DEAF=S△ADC
由勾股定理得:![]()
∴![]()
S四边形DEAF=S△ADC![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠ADC=90°,连接AC、BD,M、N分别是AC、BD的中点,连接MN
(1)求证:MN⊥BD.
(2)若∠DAC=62°,∠BAC=58°,求∠DMB

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=3,BC=7,AI平分∠BAC,CI平分∠ACB,将∠BAC平移,使其顶点与点I重合,则图中阴影部分的周长为( )

A.5B.8C.10D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1.2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段![]() 的两个端点均在小正方形的顶点上;
的两个端点均在小正方形的顶点上;


(1)在图1中画出以![]() 为底边的等腰直角
为底边的等腰直角![]() ,点
,点![]() 在小正方形顶点上;(2)在图2中画出以
在小正方形顶点上;(2)在图2中画出以![]() 为腰的等腰
为腰的等腰![]() ,点
,点![]() 在小正方形的顶点上,且
在小正方形的顶点上,且![]() 的面积为8.
的面积为8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点P从点A出发,以
,点P从点A出发,以![]() 的速度沿折线
的速度沿折线![]() 运动,最终回到点A,设点P的运动时间为
运动,最终回到点A,设点P的运动时间为![]() ,线段AP的长度为
,线段AP的长度为![]() ,则能够反映y与x之间函数关系的图象大致是
,则能够反映y与x之间函数关系的图象大致是![]()

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备在国庆节期间组织学生到泰山进行研学旅行,已知老师与学生一共25人参加此次研学旅行,购买门票共花费1700元,门票费用如表格所示,求参加研学旅行的老师和学生各有多少人?设老师有x人,学生有y人,则可列方程组为( )
景点 | 票价 | 开放时间 |
泰山门票 | 旺季:125元/人 淡季:100元/人 | 全天 |
说明:(1)旺季时间(2月~11月),淡季时间(12月-次年1月); (2)老年人(60岁~70岁)、学生、儿童(1.2米~1.4米)享受5折优惠; (3)教师、省部级劳模、英模、道德模范享受8折优惠; (4)现役军人、伤残军人、70岁以上老年人、残疾人,凭本人有效证件免费进山; (5)享受优惠的游客请出示本人有效证件。 | ||
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动![]() 某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
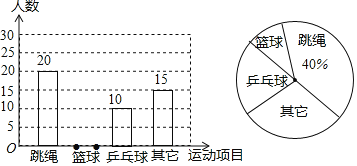
![]() 在这次调查中,喜欢篮球项目的同学有多少人?
在这次调查中,喜欢篮球项目的同学有多少人?
![]() 在扇形统计图中,“乒乓球”的百分比为多少?
在扇形统计图中,“乒乓球”的百分比为多少?
![]() 如果学校有800名学生,估计全校学生中有多少人喜欢篮球项目?
如果学校有800名学生,估计全校学生中有多少人喜欢篮球项目?
![]() 请将条形统计图补充完整;
请将条形统计图补充完整;
![]() 在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学
在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学![]() 现要从中随机抽取2名同学代表班级参加校篮球队,请运用列表或树状图求出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
现要从中随机抽取2名同学代表班级参加校篮球队,请运用列表或树状图求出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com