练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形中，，，点、分别在边，上，且，连接，将对折，点落在直线上的点处，得折痕；将对折，点落在直线上的点处，得折痕，当，分别在边，上时．若令的面积为，的长度为，则关于的函数解析式是（ ）

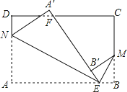
    A.

    B.

    C.

    D.

    【答案】A

    【解析】

    由对折可知△NA’E≌△NAE，可得A’E=AE=x；由对折可知△MB’E≌△MBE，可得∠MB’E=90°，B’E=EB=4-x，∠MEB’=∠MEB=60°，则MB’=.再利用即可求解.

    解：∵对折，

    ∴△NA’E≌△NAE，

    ∴A’E=AE=x，

    ∵对折，

    ∴△MB’E≌△MBE，

    ∴∠MB’E=90°，B’E=EB=4-x，∠MEB’=∠MEB=60°，

    ∴A’B’=x-4+x=2x-4，,MB’=，

    ∴，

    故选择A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校学生会准备调查六年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数．

    （1）确定调查方式时，甲同学说：“我到六年级（1）班去调查全体同学”；乙同学说：“放学时我到校门口随机调查部分同学”；丙同学说：“我到六年级每个班随机调查一定数量的同学”．请指出哪位同学的调查方式最合理．

    类别

    频数（人数）

    频率

    武术类

    0.25

    书画类

    20

    0.20

    棋牌类

    15

    b

    器乐类

    合计

    a

    1.00

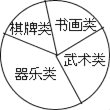
    （2）他们采用了最为合理的调查方法收集数据，并绘制了如图所示的统计表和扇形统计图．

    请你根据以上图表提供的信息解答下列问题：

    ①a=_____，b=_____；

    ②在扇形统计图中，器乐类所对应扇形的圆心角的度数是_____；

    ③若该校六年级有学生560人，请你估计大约有多少学生参加武术类校本课程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（1，0），B（2，﹣3），C（4，﹣2）．

    （1）画出△ABC关于x轴的对称图形△A1B1C1；

    （2）画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2；

    （3）如果AC上有一点P（m，n）经过上述两次变换，那么对应A2C2上的点P2的坐标是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一张一个角为30°，最小边长为4的直角三角形纸片，沿图中所示的中位线剪开后，将两部分拼成一个四边形，所得四边形的周长是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】王教授和他的孙子小强星期天一起去爬山，来到山脚下，小强让爷爷先上山，然后追赶爷爷，如图所示，两条线段分别表示小强和爷爷离开山脚的距离（米）与爬山所用时间（分）的关系（小强开始爬山时开始计时），请看图回答下列问题：

    （1）爷爷比小强先上了多少米？山顶离山脚多少米？

    （2）谁先爬上山顶？小强爬上山顶用了多少分钟？

    （3）图中两条线段的交点表示什么意思？这时小强爬山用时多少？离山脚多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某宾馆客房部有个房间供游客居住，当每个房间的定价为每天元时，所有房间刚好可以住满，根据经验发现，每个房间的定价每增加元，就会有个房间空闲，对有游客入住的房间，宾馆需对每个房间支出每天元的各种费用．设每个房间的定价增加元，每天的入住量为个，客房部每天的利润为元．

    求与的函数关系式；

    求与的函数关系式，并求客房部每天的最大利润是多少？

    当为何值时，客房部每天的利润不低于元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在四边形ABCD的边BC的延长线上取一点E，在直线BC的同侧作一个以CE为底的等腰△CEF，且满足∠B+∠F＝180°，则称三角形CEF为四边形ABCD的“伴随三角形”．

    （1）如图1，若△CEF是正方形ABCD的“伴随三角形”：

    ①连接AC，则∠ACF＝　 　；

    ②若CE＝2BC，连接AE交CF于H，求证：H是CF的中点；

    （2）如图2，若△CEF是菱形ABCD的“伴随三角形”，∠B＝60°，M是线段AE的中点，连接DM、FM，猜想并证明DM与FM的位置与数量关系．

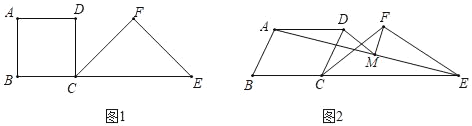
    查看答案和解析>>

    科目：初中数学 来源： 题型：

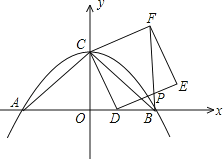
    【题目】如图，抛物线y＝﹣x2+4交x轴于点A、B，交y轴于点C，连结AC，BC，D是线段OB上一动点，以CD为一边向右侧作正方形CDEF，连结BF，交DE于点P.

    (1)试判断△ABC的形状，并说明理由；

    (2)求证：BF⊥AB.

    (3)当点D从点O沿x轴正方向移动到点B时，点E所走过的路线长为______；

    (4)探究当点D在何处时，△FBC是等腰三角形，并求出相应的BF的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究与发现：如图1所示的图形，像我们常见的学习用品--圆规．我们不妨把这样图形叫做“规形图”，

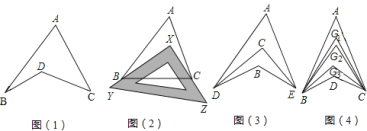
    （1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；

    （2）请你直接利用以上结论，解决以下三个问题：

    ①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，∠A=40°，则∠ABX+∠ACX等于多少度；

    ②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE=40°，∠DBE=130°，求∠DCE的度数；

    ③如图4，∠ABD，∠ACD的10等分线相交于点G1、G2…、G9，若∠BDC=133°，∠BG1C=70°，求∠A的度数．

    查看答案和解析>>

    同步练习册答案