练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】图 1、图 2 均是 6×6 的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为 1，点 A、B、C、D 均在格点上．在图 1、图 2 中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法．

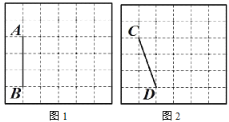
    （1）在图 1 中以线段 AB 为边画一个△ABM，使∠ABM=45°，且△ABM 的面积为 6；

    （2）在图 2 中以线段 CD 为边画一个四边形 CDEF，使∠CDE＝∠CFE=90°，且四边形 CDEF 的面积为 8．

    【答案】（1）见解析；（2）见解析.

    【解析】

    （1）根据∠ABM=45°可确定M所在直线，然后结合面积为6可得M点位置；

    （2）根据∠CDE＝90°且点E在格点上可得E点位置，然后根据∠CFE＝90°，利用直径所对的圆周角是90°结合四边形面积为8确定出点F位置即可.

    解：（1）如图1所示，△ABM即为所求；

    （2）如图2所示，四边形CDEF即为所求.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图①，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝40°，连接BD、CE．将△ADE绕点A旋转，BD、CE也随之运动．

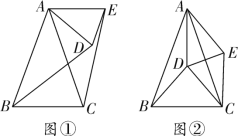
    （1）求证：BD＝CE；

    （2）在△ADE绕点A旋转过程中，当AE∥BC时，求∠DAC的度数；

    （3）如图②，当点D恰好是△ABC的外心时，连接DC，判断四边形ADCE的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形中，，将沿射线平移得到，连接，则的最小值是_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，，，点是的中点，点在边上，将沿翻折，使点落在点处，当时，________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与直线分别相交于，两点，且此抛物线与轴的一个交点为，连接，．已知，．

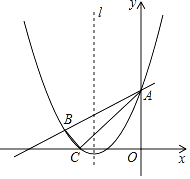
    （1）求抛物线的解析式；

    （2）在抛物线对称轴上找一点，使的值最大，并求出这个最大值；

    （3）点为轴右侧抛物线上一动点，连接，过点作交轴于点，问：是否存在点使得以，，为顶点的三角形与相似？若存在，请求出所有符合条件的点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系，点 O 是原点，直线 y x 6分别交 x 轴，y 轴于点 B，A，经过点 A 的直线 y x b 交 x 轴于点 C．

    　　

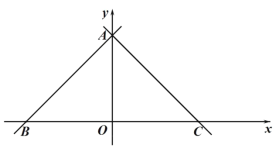
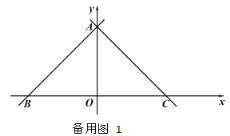
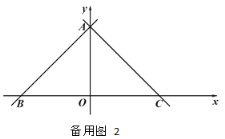
    （1）求 b 的值 ；

    （2）点 D 是线段 AB 上的一个动点，连接 OD，过点 O 作 OE⊥OD 交 AC 于点 E，连接DE，将△ODE 沿 DE 折叠得到△FDE，连接 AF．设点 D 的横坐标为 t，AF 的长为 d，当t＞ 3 时，求 d 与 t 之间的函数关系式（不要求写出自变量 t 的取值范围）；

    （3）在（2）的条件下，DE 交 OA 于点 G，且 tan∠AGD=3.点 H 在 x 轴上（点 H 在点O 的右侧），连接 DH，EH，FH，当∠DHF=∠EHF 时，请直接写出点 H 的坐标，不需要写出解题过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，以的边为直径作，点C在上，是的弦，，过点C作于点F，交于点G，过C作交的延长线于点E．

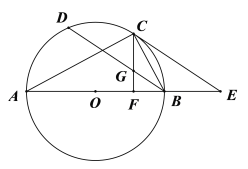
    （1）求证：是的切线；

    （2）求证：；

    （3）若，，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小军同学在学校组织的社会实践活动中，负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：x），并绘制了样本的频数分布表如下：

    月均用水量

    2≤x＜3

    3≤x＜4

    4≤x＜5

    5≤x＜6

    6≤x＜7

    7≤x＜8

    8≤x＜9

    频数

    2

    12

    ①

    10

    ②

    3

    2

    百分比

    4%

    24%

    30%

    20%

    ③

    6%

    4%

    （1）请根据题中已有的信息补全频数分布表：① ；② ；③

    （2）如果家庭月均用水量在5≤x＜8范围内为中等用水量家庭，请你通过样本估计，总体中的中等用水量家庭大约有多少户？

    （3）记月均用水量在2≤x＜3范围内的两户为a1，a2，在8≤x＜9范围内的2户为b1，b2，现从这4户家庭中任意抽取2户，请你通过列表或画树状图求出抽取的2户家庭来自不同范围的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图①、图②均是8×8的正方形网格，每个小正方形的顶点称为格点，点A、B、M、N均落在格点上，在图①、图②给定的网格中按要求作图．

    （1）在图①中的格线MN上确定一点P，使PA与PB的长度之和最小

    （2）在图②中的格线MN上确定一点Q，使∠AQM＝∠BQM．

    要求：只用无刻度的直尺，保留作图痕迹，不要求写出作法．

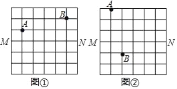
    查看答案和解析>>

    同步练习册答案