
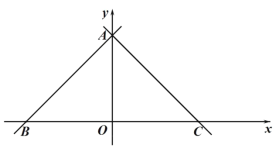
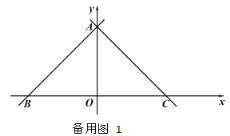
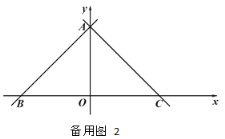
【题目】如图,在平面直角坐标系,点 O 是原点,直线 y x 6分别交 x 轴,y 轴于点 B,A,经过点 A 的直线 y x b 交 x 轴于点 C.
(1)求 b 的值 ;
(2)点 D 是线段 AB 上的一个动点,连接 OD,过点 O 作 OE⊥OD 交 AC 于点 E,连接DE,将△ODE 沿 DE 折叠得到△FDE,连接 AF.设点 D 的横坐标为 t,AF 的长为 d,当t> 3 时,求 d 与 t 之间的函数关系式(不要求写出自变量 t 的取值范围);
(3)在(2)的条件下,DE 交 OA 于点 G,且 tan∠AGD=3.点 H 在 x 轴上(点 H 在点O 的右侧),连接 DH,EH,FH,当∠DHF=∠EHF 时,请直接写出点 H 的坐标,不需要写出解题过程.
【答案】(1)b=6;(2)d=6+2t;(3)H点的坐标为(2,0)或(10,0).
【解析】
(1)由y=x+6求得A点坐标,再将A点坐标代入y=x+b中,便可求得b;
(2)过点D分别作DM⊥x轴于点M,DN⊥y轴于点N,过点F作FR⊥AF交AE于点R,可证明四边形DMON为矩形,再证△AOD≌△COE(ASA),用t表示AD,然后证明△ADF≌△REF(AAS),进而用t表示AR,问题便可迎刃而解;
(3)分两种情况解答:第一种情况,当FH平分∠DHE时,连接OF,过E作EK⊥x轴于点K,作EL⊥y轴于点L,设正方形ODFE的外接圆交x轴于点H,证明△ODM≌△EOK(AAS),用t表示出EL,OL,再由tan∠AGD=3,便可用t表示GN,GL,由OA=6列出t的方程求得t,便可求得H点坐标;第二种情况,当∠DHF与∠EHF重合时,延长DE与x轴交于点H,求出DE与x轴的交点坐标便可.
解:(1)令x=0,得y=x+6=6,
∴A(0,6),
把A(0,6)代入y=x+b中,得b=6;
(2)令y=0,得y=x+6=0,则x=6,
∴B(6,0),
∵点D的横坐标为t,
∴D(t,t+6),
令y=0,得y=x+6=0,x=6,
∴C(6,0),
∵OA=OB=6,
∴∠OAB=∠OBA=45°,
同理∠OAC=∠OCA=45°,
∴∠BAC=90°,
在Rt△AOC中,AC=![]() OA=
OA=![]() ,
,
如图1,过点D分别作DM⊥x轴于点M,DN⊥y轴于点N,
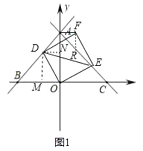
∵∠DMO=∠MON=∠OND=90°,
∴四边形DMON为矩形,
∴DN=OM=t,
在Rt△ADN中,∠DAN=45°,AD=![]() ,
,
∵∠AOD+∠AOE=90°,∠COE+∠AOE=90°,
∴∠AOD=∠COE,
又∵∠OAD=∠OCE=45°,OA=OC,
∴△AOD≌△COE(ASA),
∴OD=OE,AD=CE=![]() ,
,
∵△DFE和△DOE关于DE对称,
∴DF=OD=OE=EF,∠DFE=∠DOE=90°,
过点F作FR⊥AF交AE于点R,
∵∠AFD+∠DFR=90°,∠RFE+∠DFR=90°,
∴∠AFD=∠RFE,
∵∠ERF=∠RAF+∠AFR=∠RAF+90°,∠DAF=∠RAF+∠DAR=∠RAF+90°,
∴∠ERF=∠DAF,
∴△ADF≌△REF(AAS),
∴AF=RF,AD=RE=![]() ,
,
∴∠FAR=∠FRA,
又∵∠FAR+∠FRA═90°,
∴∠FAR=∠FRA=45°,
在Rt△AFR中,AR=ACCEER=![]() ,AF=
,AF=![]() AR=6+2t,
AR=6+2t,
∴d=6+2t;
(3)如图2,连接OF,过E作EK⊥x轴于点K,,作EL⊥y轴于点L,
由(2)可得四边形ODFE是正方形,设正方形ODFE的外接圆交x轴于点H,
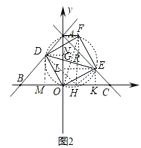
∴∠DOM+∠ODM=∠DOM+∠EOK=90°,
∴∠ODM=∠EOK,
∵∠OMD=∠EKO=90°,OD=EO,
∴△ODM≌△EOK(AAS),
∴EK=OM=DN=OL=t,LE=OK=DM=6+t,
∵tan∠AGD=3,DN=t,
∴![]() ,即
,即![]() ,
,
∴GN=![]() ,GL=
,GL=![]() ,
,
∴OA=OL+GL+GN+AN=![]() ,
,
∵OA=6,
∴2t+2=6,
∴t=2,
∴AF=6+2t═2,
∵OF是正方形ODFE的外接圆的直径,
∴FH⊥x轴,∠DHF=∠DOF=∠EOF=45°=∠EHF,
∴H(2,0)满足条件;
如图3,延长DE与x轴交于点H,则∠DHF=∠EHF,
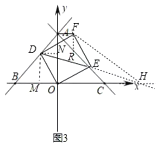
由以上知D(2,4),E(4,2),
设直线DE的解析式为:y=kx+b(k≠0),
则![]() ,解得:
,解得: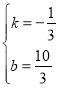 ,
,
∴直线DE的解析式为:![]() ,
,
当y=0时,得![]() ,
,
解得:x=10,
∴H(10,0),
综上,H点的坐标为(2,0)或(10,0).


科目:初中数学 来源: 题型:
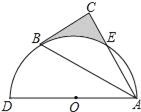
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,弧BE的长为![]() π,则图中阴影部分的面积为( )
π,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
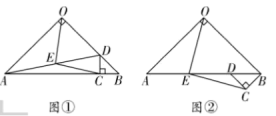
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图 1、图 2 均是 6×6 的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为 1,点 A、B、C、D 均在格点上.在图 1、图 2 中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
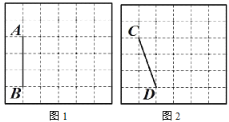
(1)在图 1 中以线段 AB 为边画一个△ABM,使∠ABM=45°,且△ABM 的面积为 6;
(2)在图 2 中以线段 CD 为边画一个四边形 CDEF,使∠CDE=∠CFE=90°,且四边形 CDEF 的面积为 8.
查看答案和解析>>
科目:初中数学 来源: 题型:
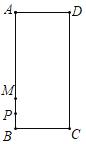
【题目】如图,矩形ABCD中,动点P沿B→A→D→C→B路线运动,点M是AB边上的一点,且MB=![]() AB,已知AB=4,BC=2,AP=2MP,则点P到边AD的距离为_______.
AB,已知AB=4,BC=2,AP=2MP,则点P到边AD的距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AE平分∠BAC交BC于E,CD⊥AE交AE延长线于D,连接BD,若BD=CD,⊙O是以AE为直径的△ABE的外接圆,与AC交于点H.

(1)求证:BD为⊙O的切线;
(2)设⊙O的半径为1,BF平分∠ABC交AE于G,交⊙O于F;
①求![]() 的值.
的值.
②求BE2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com