
����Ŀ����֪����ͼ���ı���ABCD�У�˳����������е�E��F��G��H�õ����ı���EFGH�����ı���ABCD���е��ı��Σ�
��1���ı���EFGH����״��______��֤����Ľ��ۣ�
��2������̽����ͬ�ı��ε��е��ı��ε���״��
�ٵ��ı���ABCD��Ϊƽ���ı���ʱ�������е��ı�����______��
�ڵ��ı���ABCD��Ϊ����ʱ�������е��ı�����______��
�۵��ı���ABCD��Ϊ����ʱ�������е��ı�����______��
�ܵ��ı���ABCD��Ϊ������ʱ�������е��ı�����______��
��3���������Ϲ۲�̽���������ܽ��е��ı��ε���״����ԭ�ı��ε�ʲô���ʾ����ģ�
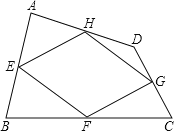
���𰸡���1���ı���EFGH��ƽ���ı��Σ�����������2����ƽ���ı��Σ������Σ��۾��Σ��������Σ�
��������
(1)����BD��������������λ�߶����Ƴ������ı��ζԱ�ƽ������ȣ���Ϊƽ���ı��Σ�
(2)Ӧ����������λ�߶����������ε���λ�ߵ��ڵ����ߵ�һ����������ƽ���ı��ε��ж������ε��ж������ε��ж��������ε��ж�����⼴�ɣ�
(3)�����Ϸ����֪���е��ı��ε���״����ԭ�ı��εĶԽ��ߵĴ�С��ϵ��λ�ù�ϵ�����ģ�
(1)�ı���EFGH��ƽ���ı��Σ�֤�����£�
��ͼ1������BD��
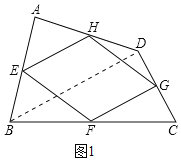
��E��H�ֱ���AB��AD���е㣬
��EH����ABD����λ�ߣ�
��EH=![]() BD��EH��BD��
BD��EH��BD��
ͬ����FG=![]() BD��FG��BD��
BD��FG��BD��
��EH=FG��EH��FG��
���ı���EFGH��ƽ���ı��Σ�
�ʴ�Ϊ��ƽ���ı��Σ�
(2)��ͬ���ã����ı���ABCD��Ϊƽ���ı���ʱ�������е��ı����ǣ�ƽ���ı��Σ�
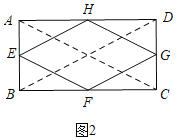
����ͼ2������AC��BD��
���ı���ABCD�Ǿ��Σ�
��AC=BD��
��EF=![]() AC��EH=
AC��EH=![]() BD��
BD��
��EF=EH��
���ı���EFGH�����Σ�
�ۡ��ı���EFGH�����Σ�
��AC��BD��
���FEH=90����
���ı���ABCD�Ǿ��Σ�
�ܡ��ı���ABCD�������Σ�
��AC=BD��AC��BD��
���ı���EFGH�������Σ�
(3)�����Ϸ����֪���е��ı��ε���״����ԭ�ı��εĶԽ��ߵĴ�С��ϵ��λ�ù�ϵ�����ģ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��һ����Ϊ2x����Ϊ2y�ij����Σ���ͼ�������ü��������ĸ���ȫ��ͬ��С�����Σ�Ȼ��ͼ2��ʾƴ��һ�������Σ�
��1������Ϊͼ2�е���Ӱ���ֵ������εı߳�����
��2���������ֲ�ͬ�ķ�����ͼ2����Ӱ���ֵ������
����1�� ����2��
��3������ͼ2����д��������������ʽ֮��ĵ�����ϵ��
����ʽ����x+y��2����x-y��2��4xy��
��4�����ݣ�3�����еĵ�����ϵ������������⣺
��x+y=4��xy=3����x-y��2=
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪ���κ���y=ax2+bx+c��a��0����ͼ��������˵������a��0 ��2a+b=0 ��a+b+c��0 �ܵ���1��x��3ʱ��y��0��������ȷ�ĸ���Ϊ��������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̶�м�2017��ɹ�����ȫ����������֮����������ȫ���������У�ijС��������Ӧ��������С���ڰ�װ�����������ܰ��ʾ�ƺ������䣬������2����ܰ��ʾ�ƺ�3�������乲��550Ԫ����������ĵ�������ܰ��ʾ�Ƶ��۵�3����
��1������ܰ��ʾ�ƺ�������ĵ��۸��Ƕ���Ԫ��
��2����С��������Ҫ����48�������䣬���������ܰ��ʾ�ƺ������乲100�����ҷ��ò�����10000Ԫ�������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���

����������x���һ������Ϊ��3��0�����ں���y=ax2+bx+c�����ֵΪ6���������ߵĶԳ�����ֱ��![]() �����ڶԳ�����࣬y��x����������ϱ���֪������˵������ȷ����____________������д��ţ�
�����ڶԳ�����࣬y��x����������ϱ���֪������˵������ȷ����____________������д��ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A(1��1)��B(��1��1)��C(��1����2)��D(1����2)���ְ�һ����Ϊ2 018����λ������û�е��Ե�ϸ��(�ߵĴ�ϸ���Բ���)��һ�˹̶��ڵ�A��������A��B��C��D��A�����Ĺ��ɽ������ı���ABCD�ı��ϣ���ϸ����һ������λ�õĵ��������________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA����3��5����B����2��1����C����1��3����
��1��������ABC����x��ĶԳ�ͼ����A1B1C1��
��2��������A1B1C1��x������ƽ��4����λ���Ⱥ�õ�����A2B2C2��
��3�����AC����һ��M��a��b�������������α任����ô��ӦA2C2�ϵĵ�M2�������� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���֪A(2��2)��B(4��0)������x����ȡ��C��ʹ��ABCΪ���������Σ������������ĵ�C�ĸ�����( )
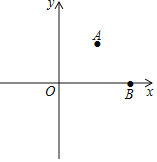
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С���ӱ�������ͼ��ݳ���������ͬ����·������������С������һ��·�̺�С����ʼ��������С������С��150��ʱ��С��ͣ�ڴ˵صȺ�С��������������һ����С��ԭ�����ٶ���������������ͼ����ӳ����������·��y���ף�������ʱ��x���룩֮��Ĺ�ϵ��������������������⣺
(1)�����е��Ա�����________���������_________��
(2) С��������________�ף�С�����ٶ�Ϊ________��/�룻
(3) ͼ��a��________�ף�С����;�еȺ�С����ʱ����________�룻
(4)С����A�ܵ�B��ε��ٶ�Ϊ________��/�룻
(5)���b��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com