
【题目】校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载.某中学九年级数学活动小组进行了测试汽车速度的实验,如图,先在笔直的公路l旁选取一点A,在公路l上确定点B、C,使得AC⊥l,∠BAC=60℃,再在AC上确定点D,使得∠BDC=75°,测得AD=40米,已知本路段对校车限速是50千米/时,测得某校车从B到C匀速行驶用时10秒。
(1)、求CD的长。(结果保留根号)
(2)、问这辆车在本路段是否超速?请说明理由(参考数据:![]() =1.41,
=1.41,![]() =1.73
=1.73

【答案】(1)、20![]() ;(2)、没有超速.
;(2)、没有超速.
【解析】
试题分析:(1)、过点D作DE⊥AB于点E,根据题意得出△CBD≌△EBD,则CD=DE,根据Rt△ADE中∠A=60°,AD=40米得出DE的长度;(2)、根据题意得出AC的长度,根据Rt△ABC得出BC的长度,然后求出速度.
试题解析:(1)、过点D作DE⊥AB于点E,∵∠CDB=75°,∠BAC=60°,∴∠CBD=15°,∠EBD=15°。
在Rt△CBD和Rt△EBD中,∵∠CBD=∠EBD,∠DCB =∠DEB,BD=BD, ∴△CBD≌△EBD(AAS)。
∴CD=DE。在Rt△ADE中,∠A=60°,AD=40米, ∴DE=ADsin60°=20![]() 米,∴CD=20
米,∴CD=20![]() 米
米
(2)、∵AD=40米,CD=20![]() 米∴AC=AD+CD=(40+20
米∴AC=AD+CD=(40+20![]() )米,
)米,
在Rt△ABC中,BC=ACtan∠A=(40![]() +60)米,
+60)米,
∴速度=![]() ≈12.92(米/秒)。 ∵12.92米/秒=46.512千米/小时<50千米/时,∴该车没有超速。
≈12.92(米/秒)。 ∵12.92米/秒=46.512千米/小时<50千米/时,∴该车没有超速。


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】某中学为了筹备校庆活动,准备印制一批校庆纪念册.该纪念册分A、B两种,每册都需要10张8K大小的纸,其中A纪念册有4张彩色页和6张黑白页组成;B纪念册有6张彩色页和4张黑白页组成.印制这批纪念册的总费用由制版费和印制费两部分组成,制版费与印数无关,价格为:彩色页300元∕张,黑白页50元∕张;印制费与总印数的关系见下表.
总印数a(单位:千册) | 1≤a<5 | 5≤a<10 |
彩色(单位:元∕张) | 2.2 | 2.0 |
黑白(单位:元∕张) | 0.7 | 0.5 |
(1)印制这批纪念册的制版费为元.
(2)若印制A、B两种纪念册各2千册,则共需多少费用?
(3)如果该校共印制了A、B两种纪念册6千册,一共花费了75500元,则该校印制了A、B两种纪念册各多少册?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年舌尖上的浪费让人触目惊心,据统计中国每年浪费的食物总量折合粮食约499.5亿千克,这个数用科学记数法应表示为( )
A. 4.995×1010B. 49.95×1010
C. 0.4995×1011D. 4.995×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.

(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,点O也是正方形A′B′C′O的一个顶点,两个正方形的边长都等于1,当正方形A′B′C′O绕顶点O转动时,两个正方形重叠部分的面积大小有什么规律?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.
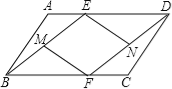
(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com