
【题目】在平面直角坐标系xOy中,点P和图形W的“中点形”的定义如下:对于图形W上的任意一点Q,连结PQ,取PQ的中点,由所以这些中点所组成的图形,叫做点P和图形W的“中点形”.
已知C(-2,2),D(1,2),E(1,0),F(-2,0).
(1)若点O和线段CD的“中点形”为图形G,则在点![]() ,
,![]() ,
,![]() 中,在图形G上的点是 ;
中,在图形G上的点是 ;
(2)已知点A(2,0),请通过画图说明点A和四边形CDEF的“中点形”是否为四边形?若是,写出四边形各顶点的坐标,若不是,说明理由;
(3)点B为直线y=2x上一点,记点B和四边形CDEF的中点形为图形M,若图形M与四边形CDEF有公共点,直接写出点B的横坐标b的取值范围.
【答案】(1)![]() ,
,![]() ;(2)点A和四边形CDEF的“中点形”是四边形,各顶点的坐标为:(0,0)、(0,1)、(
;(2)点A和四边形CDEF的“中点形”是四边形,各顶点的坐标为:(0,0)、(0,1)、(![]() ,0)、(
,0)、(![]() ,1);(3)-1≤b≤0或 1≤b≤2.
,1);(3)-1≤b≤0或 1≤b≤2.
【解析】
(1)依照题意画出图形,观察图形可知点O和线段CD的中间点所组成的图形是线段C′D′,根据点A,C,D的坐标,利用中点坐标公式可求出点C′,D′的坐标,进而可得出结论;
(2)画出图形,观察图形可得出结论;
(3)利用一次函数图象上点的坐标特征可得出点B的坐标为(n,2n),依照题意画出图形,观察图形可知:点B和四边形CDEF的中间点只能在边EF和DE上,当点B和四边形CDEF的中间点在边EF上时,利用四边形CDEF的纵坐标的范围,可得出关于n的一元一次不等式组,解之即可得出n的取值范围;当点B和四边形CDEF的中间点在边DE上时,由四边形CDEF的横、纵坐标的范围,可得出关于n的一元一次不等式组,解之即可得出n的取值范围.综上,此题得解.
解:(1)如图:点O和线段CD的中间点所组成的图形G是线段C′D′,
由题意可知:点C′为线段OC的中点,点D′为线段OD的中点.
∵点C的坐标为(-2,2),点D的坐标为(1,2),
∴点C′的坐标为(-1,1),点D′的坐标为(![]() ,1),
,1),
∴点O和线段CD的中间点所组成的图形G即线段C′D′的纵坐标是1,横坐标-1≤x≤![]() ,
,
∴点![]() ,
,![]() ,
,![]() 中,在图形G上的点是
中,在图形G上的点是![]() ,
,![]() ;
;
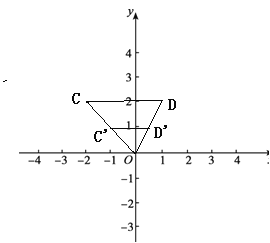
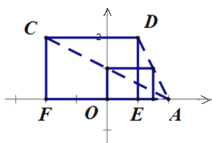
(2)点A和四边形CDEF的“中点形”是四边形.
各顶点的坐标为:(0,0)、(0,1)、(![]() ,0)、(
,0)、(![]() ,1).
,1).
(3)∵点B的横坐标为b,
∴点B的坐标为(b,2b).
当点B和四边形CDEF的中间点在边EF上时,有![]() ,
,
解得:
当点B和四边形CDEF的中间点在边DE上时,有![]() ,
,
解得:1≤b≤2,
综上所述:点B的横坐标b的取值范围为-1≤b≤0 或 1≤b≤2.
故答案为:(1)![]() ,
,![]() ;(2)点A和四边形CDEF的“中点形”是四边形,各顶点的坐标为:(0,0)、(0,1)、(
;(2)点A和四边形CDEF的“中点形”是四边形,各顶点的坐标为:(0,0)、(0,1)、(![]() ,0)、(
,0)、(![]() ,1);(3)-1≤b≤0或 1≤b≤2.
,1);(3)-1≤b≤0或 1≤b≤2.


科目:初中数学 来源: 题型:
【题目】已知如图:点(1,3)在函数y=![]() (x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=
(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=![]() (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(1)求k的值;
(2)求点A的坐标;(用含m代数式表示)
(3)当∠ABD=45°时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2)请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标.
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.
(3)画出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°, AC=4.5cm. M是边AC上的一个动点,连接MB,过点M作MB的垂线交AB于点N. 设AM=x cm,AN=y cm.(当点M与点A或点C重合时,y的值为0)
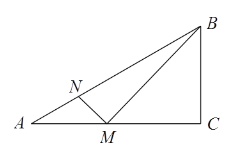
探究函数y随自变量x的变化而变化的规律.
(1) 通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
y/cm | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 1.7 | 1.6 | 1.2 | 0 |
(要求:补全表格,相关数值保留一位小数)
(2)建立平面直角坐标系xOy,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当AN=![]() AM时,AM的长度约为 cm(结果保留一位小数).
AM时,AM的长度约为 cm(结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)所示).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成的记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若EF=4,则S1+S2+S3的值是( )
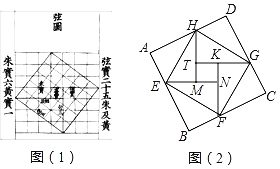
A.32B.38C.48D.80
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
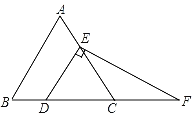
(1)求∠F的度数;
(2)若CD=4,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )

A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
【答案】D
【解析】试题分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得MN∥AB,MN=![]() AB,再根据相似三角形的判定解答.
AB,再根据相似三角形的判定解答.
试题解析:∵M、N分别是AC,BC的中点
∴MN∥AB,MN=![]() AB,
AB,
∴AB=2MN=2×12=24m
△CMN∽△CAB
∵M是AC的中点
∴CM=MA
∴CM:MA=1:1
故描述错误的是D选项.
故选D.
考点:1.三角形中位线定理;2.相似三角形的应用.
【题型】单选题
【结束】
10
【题目】若关于![]() 的一元二次方程
的一元二次方程![]() +x-3m=0有两个不相等的实数根,则
+x-3m=0有两个不相等的实数根,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.
(1)求点A的坐标和抛物线的表达式;
(2)当AE:EP=1:2时,求点E的坐标;
(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.
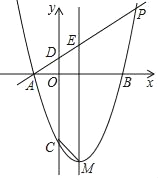
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com