
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
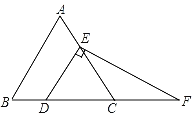
(1)求∠F的度数;
(2)若CD=4,求EF的长.
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.

(1)求证:DA∥BC;
(2)猜想线段DF、AF的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
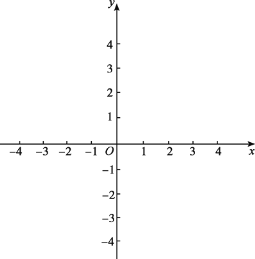
【题目】在平面直角坐标系xOy中,点P和图形W的“中点形”的定义如下:对于图形W上的任意一点Q,连结PQ,取PQ的中点,由所以这些中点所组成的图形,叫做点P和图形W的“中点形”.
已知C(-2,2),D(1,2),E(1,0),F(-2,0).
(1)若点O和线段CD的“中点形”为图形G,则在点![]() ,
,![]() ,
,![]() 中,在图形G上的点是 ;
中,在图形G上的点是 ;
(2)已知点A(2,0),请通过画图说明点A和四边形CDEF的“中点形”是否为四边形?若是,写出四边形各顶点的坐标,若不是,说明理由;
(3)点B为直线y=2x上一点,记点B和四边形CDEF的中点形为图形M,若图形M与四边形CDEF有公共点,直接写出点B的横坐标b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
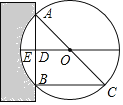
A. 13寸 B. 20寸 C. 26寸 D. 28寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四根长度分别为3,4,5,x(x为正整数)的木棒,从中任取三根,首尾顺次相接都能组成一个三角形则组成的三角形的周长( )
A.最小值是11B.最小值是12C.最大值是14D.最大值是15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题探究)
将三角形![]() 纸片沿
纸片沿![]() 折叠,使点A落在点
折叠,使点A落在点![]() 处.
处.
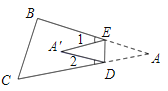
(1)如图,当点A落在四边形![]() 的边
的边![]() 上时,直接写出
上时,直接写出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
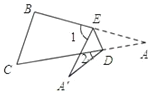
(2)如图,当点A落在四边形![]() 的内部时,求证:
的内部时,求证:![]() ;
;
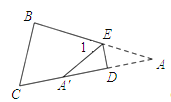
(3)如图,当点A落在四边形![]() 的外部时,探索
的外部时,探索![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(拓展延伸)
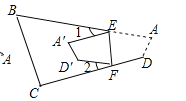
(4)如图,若把四边形![]() 纸片沿
纸片沿![]() 折叠,使点A、D落在四边形
折叠,使点A、D落在四边形![]() 的内部点
的内部点![]() 、
、![]() 的位置,请你探索此时
的位置,请你探索此时![]() ,
,![]() ,
,![]() ,
,![]() 之间的数量关系,写出你发现的结论,并说明理由.
之间的数量关系,写出你发现的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在菱形ABCD中,G是射线BC上的一动点(不与点B,C重合),连接AG,点E、F是AG上两点,连接DE,BF,且知∠ABF=∠AGB,∠AED=∠ABC.
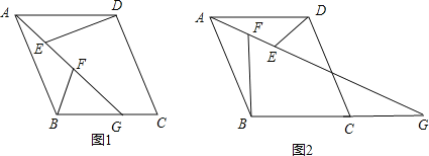
(1)若点G在边BC上,如图1,则:
①△ADE与△BAF______;(填“全等”或“不全等”或“不一定全等”)
②线段DE、BF、EF之间的数量关系是______;
(2)若点G在边BC的延长线上,如图2,那么上面(1)②探究的结论还成立吗?如果成立,请给出证明;如果不成立,请说明这三条线段之间又怎样的数量关系,并给出你的证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com