
����Ŀ����֪��������ABCD�У�G������BC�ϵ�һ���㣨�����B��C�غϣ�������AG����E��F��AG�����㣬����DE��BF����֪��ABF=��AGB����AED=��ABC��
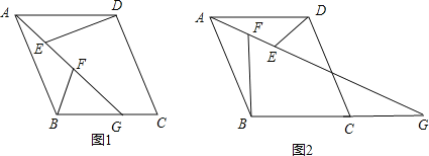
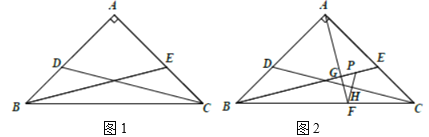
��1������G�ڱ�BC�ϣ���ͼ1����
�١�ADE����BAF______�����ȫ�ȡ���ȫ�ȡ���һ��ȫ�ȡ���
���߶�DE��BF��EF֮���������ϵ��______��
��2������G�ڱ�BC���ӳ����ϣ���ͼ2����ô���棨1����̽���Ľ��ۻ���������������������֤�����������������˵���������߶�֮����������������ϵ�����������֤����
���𰸡���1����ȫ�ȣ���DE=BF+EF����2��DE=BF-EF��������
��������
(1)���������ε����ʵõ�AB=AD��AD��BC����ƽ���ߵ����ʵõ���BGA=��DAE�����������õ���BAF=��ADE�������ABF=��DAE������ȫ�������ε��ж��������ɵõ����ۣ�
������ȫ�������ε����ʵõ�AE=BF��DE=AF�������߶εĺͲ�ɵõ����ۣ�
(2)��(1)ͬ��֤��ABF�ա�DAE��AE=BF��DE=AF����AF=AE-EF=BF-EF�ɵô𰸣�
(1)�١��ı���ABCD�����Σ�
��AB=AD��AD��BC��
���BGA=��DAE��
�ߡ�ABC=��AED��
���BAF=180![]() -��ABC -��BGA =180
-��ABC -��BGA =180![]() -��AED -��DAE =��ADE��
-��AED -��DAE =��ADE��
�ߡ�ABF=��BGF����BGA=��DAE��
���ABF=��DAE��
��AB=DA��
���ABF�ա�DAE(ASA)��
�ڡߡ�ABF�ա�DAE��
��AE=BF��DE=AF��
��AF=AE+EF=BF+EF��
��DE=BF+EF��
�ʴ�Ϊ��ȫ�ȣ�DE=BF+EF��
(2)DE=BF-EF��
��ͼ��
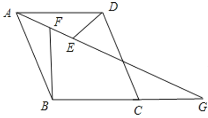
���ı���ABCD�����Σ�
��AB=AD��AD��BC��
���BGA=��DAE��
�ߡ�ABC=��AED��
���BAF=180![]() -��ABC -��BGA =180
-��ABC -��BGA =180![]() -��AED -��DAE =��ADE��
-��AED -��DAE =��ADE��
�ߡ�ABF=��BGF����BGA=��DAE��
���ABF=��DAE��
��AB=DA��
���ABF�ա�DAE(ASA)��
��AE=BF��DE=AF��
��AF=AE-EF=BF-EF��
��DE=BF-EF



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У���D��E�ֱ��ڱ�BC��AC�ϣ�DE��AB������E��EF��DE����BC���ӳ����ڵ�F��
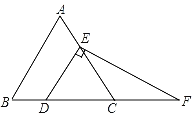
��1�����F�Ķ�����
��2����CD��4����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90������ABC=30��������ABC�Ƶ�C˳ʱ����ת����A��B��C��ʹ�õ�A��ǡ������AB�ϣ�����ת�Ƕ�Ϊ��������
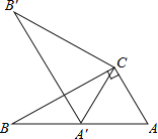
A.30��B.60��C.90��D.150��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
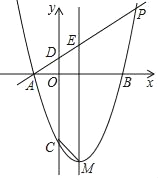
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=x2+bx+c�ĶԳ���Ϊֱ��x=1����������x�ύ��A��B���㣨��A�ڵ�B����ࣩ����AB=4����P����������λ�ڵ�һ���ĵ㣬ֱ��AP��y�ύ�ڵ�D����Գ��ύ�ڵ�E�����P�ĺ�����Ϊt��
��1�����A������������ߵı���ʽ��
��2����AE��EP=1��2ʱ�����E�����ꣻ
��3���������ߵĶ���ΪM����y��Ľ���ΪC�����ı���CDEM�ǵ�������ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
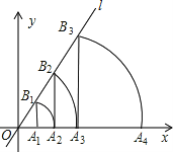
����Ŀ����ֱ������ϵ�У�ֱ��lΪy=![]() x������A1��1��0����A1B1��x�ᣬ��ֱ��l���ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���ڵ�A2������A2B2��x�ᣬ��ֱ��l�ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���ڵ�A3����������������������ȥ�����A20��������______��
x������A1��1��0����A1B1��x�ᣬ��ֱ��l���ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���ڵ�A2������A2B2��x�ᣬ��ֱ��l�ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���ڵ�A3����������������������ȥ�����A20��������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�����װ�кڡ���������ɫ����30ֻ����Щ�����ɫ��������ȫ��ͬ�����Ⱥ�С��������ʵ�飬���Ӻ������������һֻ�������ɫ���ٰ���Żغ����У������ظ��������̣��±���ʵ���е�һ��ͳ�����ݣ�

��1�����Ӻ������������һֻ������������ĸ��ʵĹ���ֵΪ�� ������ȷ��0.1��
��2���������ɫ�������� ��ֻ��
��3������m����ȫһ���İ��������������ﲢҡ�ȣ��������1�����ǰ���ĸ�����0.8����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���ϣ�С����������һ�����⣺
��ͼ1���ڵ���![]() �У�
��![]() ��
��![]() ��
��![]() ����֤
����֤![]() ��
��
�ڴ�����Ļ����ϣ���ʦ���䣺
����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����̽���߶�
����̽���߶�![]() ��
��![]() ��
��![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
С��ͨ���о����֣�![]() ��
��![]() ��ij��������ϵ��
��ij��������ϵ��
С��ͨ���о����֣��������߶��е������ŵ�ͬһ��ֱ���ϣ������س�����������ͨ����һ�����������Եó����ۣ�
�Ķ�������ϣ���ش��������⣺
��1����֤![]() ��
��
��2������![]() ��
��![]() ��������ϵ����֤����
��������ϵ����֤����
��3��̽���߶�![]() ��
��![]() ��
��![]() ֮���������ϵ����֤����
֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
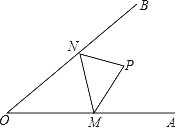
����Ŀ����ͼ����P�ǡ�AOB������һ�㣬�ҡ�AOB=40������M�͵�N�ֱ�������OA������OB�ϵĶ��㣬����PMN�ܳ�ȡ��Сֵʱ�����MPN�Ķ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=kx+b��x���ڵ�A����y���ڵ�B��ֱ��y=2x��4��x���ڵ�D����ֱ��AB�ཻ�ڵ�C��3��2����
��1������ͼ��д������x�IJ���ʽ2x��4��kx+b�Ľ⼯��
��2������A������Ϊ��5��0������ֱ��AB�Ľ���ʽ��
��3���ڣ�2���������£����ı���BODC�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com