
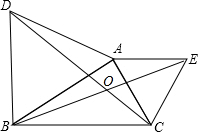
 如图,△ABD和△AEC都是等边三角形;
如图,△ABD和△AEC都是等边三角形;分析 (1)利用△ABD、△AEC都是等边三角形,求证△DAC≌△BAE,然后即可得出BE=DC;
(2)利用旋转的性质得出△DAC≌△BAE,然后即可得出BE=DC.
解答 证明:(1)∵△ABD、△AEC都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°.
∴∠DAC=∠BAC+60°,∠BAE=∠BAC+60°.
∴∠DAC=∠BAE.
在△DAC和△BAE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AE=AC}\end{array}\right.$,
∴△DAC≌△BAE(SAS),
∴BE=DC;
(2)△ABE可以看成是△ADC绕点A逆时针方向旋转60°而得到,
∵CD的对应线段是BE,
∴BE=CD.
点评 此题考查学生对全等三角形的判定与性质和等边三角形的性质的理解与掌握,掌握△DAC≌△BAE的条件是解题的关键.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点.
已知二次函数的图象经过A(3,0),B(0,-3),C(-2,5)三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+1.25b)元 | B. | (a-1.25b)元 | C. | (a+5b)元 | D. | (a-5b)元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com