

分析 (1)连接CB,根据等腰三角形的性质和三角形的外角性质解答即可;
(2)①在CE上截取CH=CA,连接FH,利用全等三角形的判定和性质解答即可;
②根据全等三角形的性质进行解答即可.
解答 证明:(1)连接CB,由AO=OB,CO⊥AB,
∴CA=CB,
∴∠A=∠CBA,
∵AC=BE,
∴BE=CB,
∴∠E=∠BCE,
∴∠A=∠CBA=∠BCE+∠E=2∠E;
(2)①在CE上截取CH=CA,连接FH,
∵∠ACF=∠ECF,CF=CF,
在△FCA与△FCH中,
$\left\{\begin{array}{l}{CH=CA}\\{∠ACF=∠ECF}\\{CF=CF}\end{array}\right.$,
∴△FCA≌△FCH,
∴AF=HF,∠A=∠CHF=∠HFE+∠E=2∠E,
∴∠HFE=∠E,
∴AF=HE,
即CE=CH+HE=CA+AF;
②在①的基础上,BE=AC,AO=OB,
∴CE=CA+AF
=BE+AO+OF
=EF-FB+OB+OF
=EF+OF+OF
=EF+2OF.
点评 此题考查了全等三角形的判定与性质和等腰三角形的判定与性质以及等腰三角形的性质;证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
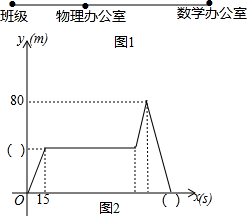 某校八(22)班同学上午第二节下课5分钟后,以2m/s的平均速度去物理老师办公室请教问题,他离班级距离y(m)与时间x(s)关系如图所示:
某校八(22)班同学上午第二节下课5分钟后,以2m/s的平均速度去物理老师办公室请教问题,他离班级距离y(m)与时间x(s)关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
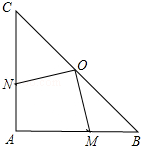 如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM.
如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com