练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    小明家、公交车站、学校在一条笔直的公路旁（小明家到这条公路的距离忽略不计）。一天，小明从家出发去上学，沿这条公路步行到公交车站恰好乘上一辆公交车，公交车沿这条路匀速行驶，小明下车时发现还有4分钟上课，于是他沿这条路跑步赶到学校（上、下车时间忽略不计），小明与家的距离s（单位：米）与他所用的时间t（单位：分钟）之间的函数关系如图所示。已知小明从家出发7分钟时与家的距离为1200米，从上车到他到达学校共用10分钟。下列说法：

    ①小明从家出发5分钟时乘上公交车

    ②公交车的速度为400米/分钟

    ③小明下公交车后跑向学校的速度为100米/分钟

    ④小明上课同有迟到。

    其中正确的个数是（  ）

    （A）1个  （B）2个 （C）3个 （D）4个


    D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    在□ABCD中，点E、F在AC上，且∠ABE=∠CDF，

    求证：BE=DF.

    （第19题）

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某班七个兴趣小组人数分别为4，4，5，x，6，6，7．已知这组数据的平均数是5，则这组数据的中位数是（　　）

    　

    A．

    7

    B．

    6

    C．

    5

    D．

    4

    　

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小明在课外学习时遇到这样一个问题：

    定义：如果二次函数y=a1x2+b1x+c1（a1≠0，a1，b1，c1是常数）与y=a2x2+b2x+c2（a2≠0，a2，b2，c2是常数）满足a1+a2=0，b1=b2，c1+c2=0，则称这两个函数互为“旋转函数”．

    求函数y=﹣x2+3x﹣2的“旋转函数”．

    小明是这样思考的：由函数y=﹣x2+3x﹣2可知，a1=﹣1，b1=3，c1=﹣2，根据a1+a2=0，b1=b2，c1+c2=0，求出a2，b2，c2，就能确定这个函数的“旋转函数”．

    请参考小明的方法解决下面问题：

    （1）写出函数y=﹣x2+3x﹣2的“旋转函数”；

    （2）若函数y=﹣x2+mx﹣2与y=x2﹣2nx+n互为“旋转函数”，求（m+n）2015的值；

    （3）已知函数y=﹣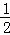（x+1）（x﹣4）的图象与x轴交于点A、B两点，与y轴交于点C，点A、B、C关于原点的对称点分布是A1，B1，C1，试证明经过点A1，B1，C1的二次函数与函数y=﹣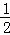（x+1）（x﹣4）互为“旋转函数．”

    　

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示的几何体是由五个小正方形体组合而成的，它的主视图是（  ）

    正面
     

       

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个扇形的半径为3cm，面积为 ,则此扇形的圆心角为          

    查看答案和解析>>

    科目：初中数学 来源： 题型：


          图1，图2是两两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，每个小正方形的顶点叫做格点.

    （1）       在图1中画出等腰直角三角形MON，使点N在格点上，且∠MON=900；

    （2）       在图2中以格点为顶点画出一个正方形ABCD，使正方形ABCD面积等于（1）中等腰直角三角形MON面积的4倍，并将正方形ABCD分割成以格点为顶点的四个全等的直角三角和一个正方形，且正方形ABCD面积没有剩余（画出一种即可）.


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点在正方形的边上，若的面积为则线段的长为        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在下列二次函数中，其图象的对称轴为的是

    A．              B．             C．          D．

    查看答案和解析>>

    同步练习册答案