
【题目】已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,A(0,2),B(﹣1,0). 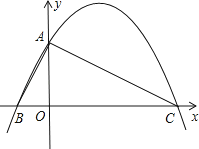
(1)求点C的坐标;
(2)求过A、B、C三点的抛物线的解析式和对称轴;
(3)设点P(m,n)是抛物线在第一象限部分上的点,△PAC的面积为S,求S关于m的函数关系式,并求使S最大时点P的坐标;
(4)在抛物线对称轴上,是否存在这样的点M,使得△MPC(P为上述(3)问中使S最大时的点)为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:在Rt△ABC中,AO⊥BC,OA=2,OB=1,
则:OC= ![]() =4,
=4,
∴C(4,0).
(2)
解:设抛物线的解析式:y=a(x+1)(x﹣4),代入点A的坐标,得:
a(0+1)(0﹣4)=2,a=﹣ ![]()
∴抛物线的解析式:y=﹣ ![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣ ![]() x2+
x2+ ![]() x+2,对称轴是:直线x=
x+2,对称轴是:直线x= ![]()
(3)
解:设直线AC的解析式为:y=kx+2,代入点C(4,0),得:
4k+2=0,k=﹣ ![]()
∴直线AC:y=﹣ ![]() x+2;
x+2;
过点P作PQ⊥x轴于H,交直线AC于Q,设P(m,﹣ ![]() m2+
m2+ ![]() m+2)、
m+2)、
∴S梯形AOHP= ![]() [2+(﹣
[2+(﹣ ![]() m2+
m2+ ![]() m+2)]m=﹣
m+2)]m=﹣ ![]() m3+
m3+ ![]() m2+2m,
m2+2m,
S△PHC= ![]() (4﹣m)(﹣
(4﹣m)(﹣ ![]() m2+
m2+ ![]() m+2)=
m+2)= ![]() m3﹣
m3﹣ ![]() m2+2m+4,
m2+2m+4,
S△AOC= ![]() ×4×2=4,
×4×2=4,
S=S梯形AOHP+S△PHC﹣S△AOC=﹣m2+4m=﹣(m﹣2)2+4,
∴当m=2,即 P(2,3)时,S的值最大
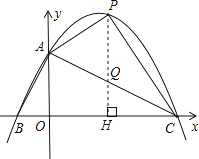
(4)
解:依题意,设M( ![]() ,b),已知P(2,3)、C(4,0),则有:
,b),已知P(2,3)、C(4,0),则有:
MP2=b2﹣6b+ ![]() 、MC2=b2+
、MC2=b2+ ![]() 、PC2=13;
、PC2=13;
当MP=MC时,b2﹣6b+ ![]() =b2+
=b2+ ![]() ,解得 b=
,解得 b= ![]() ;
;
当MP=PC时,b2﹣6b+ ![]() =13,解得 b=
=13,解得 b= ![]() ;
;
当MC=PC时,b2+ ![]() =13,解得 b=±
=13,解得 b=± ![]() ;
;
综上,存在符合条件的M点,且坐标为 ( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() )、(
)、( ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)Rt△ABC中,AO⊥BC,且知道了OA、OB的长,由射影定理能求出OC的长,也就得到了点C的坐标.(2)利用待定系数法即可确定抛物线的解析式,由x=﹣ ![]() 能求出抛物线的对称轴.(3)首先求出直线AC的解析式,过点P作x轴的垂线,交直线AC于Q,在知道抛物线和直线AC解析式的情况下,用m表示出点P、Q的坐标,两点纵坐标差的绝对值即为线段PQ的长,而S=
能求出抛物线的对称轴.(3)首先求出直线AC的解析式,过点P作x轴的垂线,交直线AC于Q,在知道抛物线和直线AC解析式的情况下,用m表示出点P、Q的坐标,两点纵坐标差的绝对值即为线段PQ的长,而S= ![]() ACPQ,据此求得关于S、m的函数关系式,根据函数的性质即可确定S最大时点P的坐标.(4)首先设出点M的坐标,然后列出△MPC的三边长,若该三角形是等腰三角形,根据①MP=MC、②MP=PC、③MC=PC列出等式求解即可.
ACPQ,据此求得关于S、m的函数关系式,根据函数的性质即可确定S最大时点P的坐标.(4)首先设出点M的坐标,然后列出△MPC的三边长,若该三角形是等腰三角形,根据①MP=MC、②MP=PC、③MC=PC列出等式求解即可.


科目:初中数学 来源: 题型:
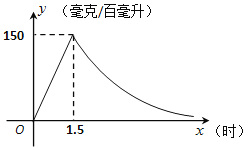
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量![]() (毫克/百毫升)与时间
(毫克/百毫升)与时间![]() (时)成正比例;1.5小时后(包括1.5小时)
(时)成正比例;1.5小时后(包括1.5小时)![]() 与
与![]() 成反比例.根据图中提供的信息,解答下列问题:
成反比例.根据图中提供的信息,解答下列问题:
(1)求一般成人喝半斤低度白酒后, ![]() 与
与![]() 之间的两个函数关系式及相应的自变量
之间的两个函数关系式及相应的自变量![]() 取值范围;
取值范围;
(2)依据人的生理数据显示,当![]() ≥80时,肝部正被严重损伤,请问喝半斤低度白酒后,肝部被严重损伤持续多少小时?
≥80时,肝部正被严重损伤,请问喝半斤低度白酒后,肝部被严重损伤持续多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李先生在2018年9月第14周星期五股市收盘时,以每股9元的价格买进某公司的股票1000股,在9月第3周的星期一至星期五,该股票每天收盘时每股的涨跌(单位:元)情况如下表:注:表中记录的数据为每天收盘价格与前一天收盘价格的变化量,星期一的数据是与上星期五收盘价格的变化量.

(1)请你判断在9月的第3周内,该股票价格收盘时,价格最高的是哪一天?
(2)在9月第3周内,求李先生购买的股票每股每天平均的收盘价格.(结果精确到百分位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知P为⊙O外一点,PA为⊙O的切线,B为⊙O上一点,且PA=PB,C为优弧 ![]() 上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.
上任意一点(不与A、B重合),连接OP、AB,AB与OP相交于点D,连接AC、BC.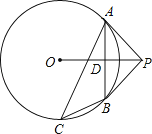
(1)求证:PB为⊙O的切线;
(2)若tan∠BCA= ![]() ,⊙O的半径为
,⊙O的半径为 ![]() ,求弦AB的长.
,求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)延长CB至G点,使得BG=DF (如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点P、Q分别是边AD和BC的中点,沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G,若BC长为3,则线段FG的长为 . 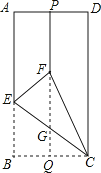
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种型号的滑板车,共花费13000元,所购进甲型车的数量不少于乙型车数量的二倍,但不超过乙型车数量的三倍.现已知甲型车每辆进价200元,乙型车每辆进价400元,设商店购进乙型车x辆.
(1)商店有哪几种购车方案?
(2)若商店将购进的甲、乙两种型号的滑板车全部售出,并且销售甲型车每辆获得利润70元,销售乙型车每辆获得利润50元,写出此商店销售这两种滑板车所获得的总利润y(元)与购进乙型车的辆数x(辆)之间的函数关系式?并求出商店购进乙型车多少辆时所获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n=![]() .
.

如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
![]() 请你根据上图填写下表:
请你根据上图填写下表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 |
| 9 | ||
乙 | 9 |
| 8 |
![]() 请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
![]() 从平均数和方差结合看;
从平均数和方差结合看;
![]() 从折线图上甲、乙两个汽车销售公司销售数量的趋势看
从折线图上甲、乙两个汽车销售公司销售数量的趋势看![]() 分析哪个汽车销售公司较有潜力
分析哪个汽车销售公司较有潜力![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com