
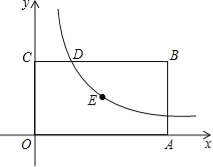
【题目】如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=![]() (x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(1)求反比例函数的解析式和点D的坐标;
(2)若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,求此直线的解析式.
【答案】(1)反比例函数解析式为y=![]() ,点D的坐标为(1,2);
,点D的坐标为(1,2);
(2)直线的解析式为y=﹣2x+4或y=﹣![]() x+
x+![]() .
.
【解析】
试题(1)根据中心对称求出点E的坐标,再代入反比例函数解析式求出k,然后根据点D的纵坐标与点B的纵坐标相等代入求解即可得到点D的坐标;
(2)设直线与x轴的交点为F,根据点D的坐标求出CD,再根据梯形的面积分两种情况求出OF的长,然后写出点F的坐标,再利用待定系数法求一次函数解析式求出直线解析式即可.
试题解析:(1)∵矩形OABC的顶点B的坐标是(4,2),E是矩形ABCD的对称中心,
∴点E的坐标为(2,1),
代入反比例函数解析式得,![]() =1,
=1,
解得k=2,
∴反比例函数解析式为y=![]() ,
,
∵点D在边BC上,
∴点D的纵坐标为2,
∴y=2时,![]() =2,
=2,
解得x=1,
∴点D的坐标为(1,2);
(2)如图,
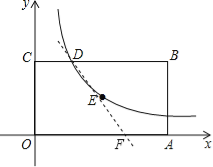
设直线与x轴的交点为F,
矩形OABC的面积=4×2=8,
∵矩形OABC的面积分成3:5的两部分,
∴梯形OFDC的面积为![]() ×8=3,
×8=3,
或![]() ×8=5,
×8=5,
∵点D的坐标为(1,2),
∴若![]() (1+OF)×2=3,
(1+OF)×2=3,
解得OF=2,
此时点F的坐标为(2,0),
若![]() (1+OF)×2=5,
(1+OF)×2=5,
解得OF=4,
此时点F的坐标为(4,0),与点A重合,
当D(1,2),F(2,0)时,![]() ,
,
解得![]() ,
,
此时,直线解析式为y=﹣2x+4,
当D(1,2),F(4,0)时,![]() ,
,
解得 ,
,
此时,直线解析式为y=﹣![]() x+
x+![]() ,
,
综上所述,直线的解析式为y=﹣2x+4或y=﹣![]() x+
x+![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了提高学生书水平.我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分.根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
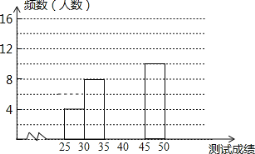
请结合图表完成下列各题:
(1)求表中a的值,并把频数分布方图补充完整;
(2)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
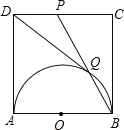
【题目】如图,AB是半圆O的直径,以AB为边在半圆同侧作正方形ABCD,点P是CD中点,BP与半圆交于点Q,连接DQ,设半圆的半径为a.
(1)判断直线DQ与半圆O的位置关系,并说明理由;
(2)求sin∠DQP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
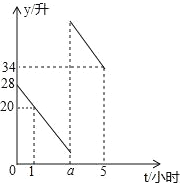
(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化校园,学校决定利用现有的2660盆甲种花卉和3000盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内,已知搭配一个A种造型需甲种花卉70盆,乙种花卉30盆,搭配一个B种造型需甲种花卉40盆,乙种花卉80盆.则符合要求的搭配方案有几种( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,某校学生会为了调查学生对雾霾天气知识的了解程度,随机抽取了该校的n名学生做了一次跟踪调查,将调查结果分为四个等级:(A)非常了解.(B)比较了解.(C)基本了解.(D)不了解,并将调查结果绘制成如下两幅不完整统计图.
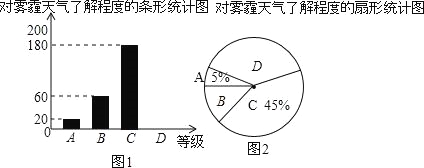
根据统计图提供的信息,解答下列问题:
(1)求n的值;
(2)在调查的n名学生中,对雾霾天气知识不了解的学生有 人,并将条形统计图补充完整.
(3)估计该校1500名学生中,对雾霾天气知识比较了解的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).
(1)点(![]() )的“双角坐标”为_____;
)的“双角坐标”为_____;
(2)若点P到x轴的距离为![]() ,则m+n的最小值为_____.
,则m+n的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明(包含设计费与印刷费),乙公司的收费与印刷卡片数量的关系如图2所示.
(1)分别写出甲乙两公司的收费y(元)与印刷数量x之间的关系式.
(2)如果你是小强,你会选择哪家公司?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(x1,0)、B(x2,0),与y轴交于点C(0,﹣x2),且x1<0<x2, ![]() ,△ABC的面积为6.
,△ABC的面积为6.
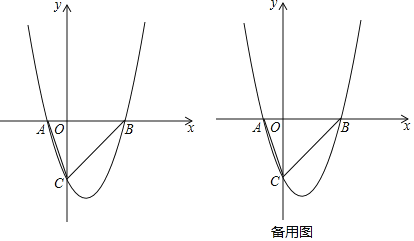
(1)求抛物线的解析式;
(2)在x轴下方的抛物线上是否存在一点M,使四边形ABMC的面积最大?若存在,请求出点M的坐标和四边形ABMC的面积最大值;若不存在,请说明理由;
(3)E为抛物线的对称轴上一点,抛物线上是否存在一点D,使以B、C、D、E为顶点的四边形为平行四边形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com