
分析 (1)根据购买一套A型课桌凳比购买一套B型课桌凳少用40元,以及购买4套A型和5套B型课桌凳共需1820元,得出等式方程求出即可;
(2)利用要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的$\frac{2}{3}$,得出不等式组,求出a的值即可,再利用一次函数的增减性得出答案即可.
解答 解:(1)设A型每套x元,则B型每套(x+40)元.
由题意得:4x+5(x+40)=1820.
解得:x=180,x+40=220.
即购买一套A型课桌凳和一套B型课桌凳各需180元、220元;
(2)设购买A型课桌凳a套,则购买B型课桌凳(200-a)套.
由题意得:$\left\{\begin{array}{l}{a≤\frac{2}{3}(200-a)}\\{180a+220(200-a)≤40880}\end{array}\right.$,
解得:78≤a≤80.
∵a为整数,
∴a=78、79、80.
∴共有3种方案,
设购买课桌凳总费用为y元,
则y=180a+220(200-a)=-40a+44000.
∵-40<0,y随a的增大而减小,
∴当a=80时,总费用最低,此时200-a=120,
即总费用最低的方案是:购买A型80套,购买B型120套.
点评 此题主要考查了一元一次方程的应用和不等式组的应用以及一次函数的增减性,根据已知得出不等式组,求出a的值是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
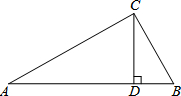 如图,在△ABC中,CD⊥AB于点D.下列条件:①BC2=BD•BA;②$\frac{AC}{AB}$=$\frac{AD}{AC}$;③CD2=AD•BD.其中能证明△ABC是直角三角形的是①②③.
如图,在△ABC中,CD⊥AB于点D.下列条件:①BC2=BD•BA;②$\frac{AC}{AB}$=$\frac{AD}{AC}$;③CD2=AD•BD.其中能证明△ABC是直角三角形的是①②③.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com