练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图图形中，既是轴对称图形又是中心对称图形的有（ ）

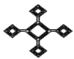
    A.1个B.2个C.3个D.4个

    【答案】A

    【解析】

    根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．

    解：从左起第1个图形，∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，但不是轴对称图形，故此选项错误；
    从左起第2个图形，∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误；
    从左起第3个图形，此图形旋转180°后不能与原图形重合，此图形不是中心对称图形，是轴对称图形，故此选项错误；
    从左起第4个图形，∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故此选项正确．
    故既是轴对称图形又是中心对称图形的有1个，
    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】求证：三角形的一条中位线与第三边上的中线互相平分．

    要求：(1)根据给出的和它的一条中位线,在给出的图形上,请用尺规作出边上的中线,交于点．不写作法,保留痕迹；

    (2)据此写出已知,求证和证明过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线交x轴于点A（-3，0）和点B，交y轴于点C（0，3）．

    （1）求抛物线的函数表达式；

    （2）若点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，求线段DQ长度的最大值．

    （3）点G是抛物线上的动点，点F在x轴上的动点，若以A，C，F，G四个点为顶点的四边形是平行四边形，求出所有满足条件的点F坐标（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校开展“江山如此多娇”为主题的地理知识竞赛活动，要求每班派出一名同学代表本班参赛．九年一班四名同学主动报名，老师为了确定最终参赛人选，对这四名同学的历次地理考试成绩进行了汇总，数据如下：

    班级里数学小组的同学对上面的数据进行了进一步的整理：

    根据以上的信息，回答下列问题：

    （1）写出上表中 ， ， ．

    （2）丙同学看到统计表，对老师说：“我的成绩方差最小，说明我的成绩最稳定，应该派我去参赛！”请问你是否同意他的观点？若你是老师，你将派谁参赛？说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD中，E，F分别为AD，AB上的点，且AE=AF，连接EF并延长，交CB的延长线于点G，连接BD．

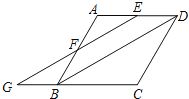
    (1) 求证：四边形EGBD是平行四边形；

    (2) 连接AG,若∠FGB=，GB=AE=3，求AG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市“上品”房地产开发公司于2010年5月份完工一商品房小区，6月初开始销售，其中6月的销售单价为0.7万元，7月的销售单价为0.72万元，且每月销售价格（单位：万元）与月份（，为整数）之间满足一次函数关系：每月的销售面积为 （单位：），其中．（，为整数）．

    （1）求与月份的函数关系式；

    （2）6~11月中，哪一个月的销售额最高？最高销售额为多少万元？

    （3）2010年11月时，因会受到即将实行的“国八条”和房产税政策的影响，该公司销售部预计12月份的销售面积会在11月销售面积基础上减少，于是决定将12月份的销售价格在11月的基础上增加，该计划顺利完成．为了尽快收回资金，2011年月公司进行降价促销，该月销售额为万元．这样12月、1月的销售额共为4618.4万元，请根据以上条件求出的值为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在中，已知， ，于点，点在直线上，，点在线段上，是的中点，直线与直线交于点．

    (1)如图，若点在线段上，线段和之间的数量关系是 ，位置关系是 ；

    (2)在(1)的条件下，当点在线段上，且时，求证：；

    (3)当点在线段的延长线上时，在线段上是否存在点，使得？若存在，求出的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列图形：

    （1）可知tanα＝，tanβ＝，用“画图法”求tan（α+β）的值，具体解法如下：

    第一步：如图1所示，构造符合题意两个“背靠背”的直角三角形；

    第二步：如图2所示，将图1中所有数据同比例扩大3倍；

    第三步：如图3所示，依托中间的Rt△ABD的各顶点构造“水平﹣﹣竖直辅助线”，构造出“一线三直角”基本相似型，并补成矩形ACEF；由图可知tan（α+β）＝　 　．

    （2）依据（1）的方法，已知tanα＝，tanβ＝，用“画图法”求tan（α+β）的值．

    （3）扩展延伸，已知tanα＝，tanβ＝，直接写出tan（α﹣β）＝　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1是一个地铁站入口的双翼闸机．如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为10cm，双翼的边缘AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30°．当双翼收起时，可以通过闸机的物体的最大宽度为(　　)

    A. (54+10) cm B. (54+10) cm C. 64 cm D. 54cm

    查看答案和解析>>

    同步练习册答案