
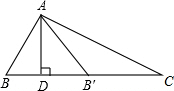
 如图,△ABC中,∠B=2∠C,AD是BC上的高,沿AD所在直线将△ABD翻折,点B落在B′处.
如图,△ABC中,∠B=2∠C,AD是BC上的高,沿AD所在直线将△ABD翻折,点B落在B′处.分析 (1)由于AD⊥BC,沿AD所在直线将△ABD翻折,点B落在B′处,则∠ADB=∠ADB′=90°,所以∠ADB+∠ADB′=180°,所以点B′在DC上.
(2)AB+BD=DC;根据三角形外角等于和它不相邻的两内角和,知∠AB′C=∠C+∠B′AC,根据折叠的性质,∠B=∠AB′D,又∠B=2∠C,所以∠C=∠CAB′,故AB′=CB′,根据折叠的性质可知,BD=B′D,AB=AB′,所以AB+BD=DC.
解答 解:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°
∵沿AD所在直线将△ABD翻折,点B落在B′处,
∴∠ADB=∠ADB′=90°,
∴所以∠ADB+∠ADB′=180°,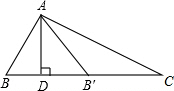
∴点B′在DC上.
(2)AB+BD=DC;
根据折叠的性质,∠B=∠AB′D,
∵∠AB′C=∠C+∠B′AC,∠B=2∠C,
∴∠C=∠CAB′,
∴AB′=CB′,
根据折叠的性质可知,BD=B′D,AB=AB′,
∴AB+BD=B′C+DB′=DC.
点评 此题主要考查了折叠的性质以及等腰三角形的判定和性质、三角形的内角和定理以及三角形外角和定理,题目的综合性很强,难度不大,解题的关键是利用方程思想解决几何图形问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{37}$ | B. | $\sqrt{13}$ | C. | $\sqrt{37}$、$\sqrt{13}$ | D. | $\sqrt{37}$、$\sqrt{13}$、5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
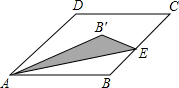 如图,已知在周长为20的菱形ABCD中,∠C=45°,点E是线段BC上一点,将△ABE沿AE所在直线翻折,使点B落在B′上,则在点E沿B→C→D运动的过程中,点B′运动的路径长是$\frac{5π}{4}$.
如图,已知在周长为20的菱形ABCD中,∠C=45°,点E是线段BC上一点,将△ABE沿AE所在直线翻折,使点B落在B′上,则在点E沿B→C→D运动的过程中,点B′运动的路径长是$\frac{5π}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
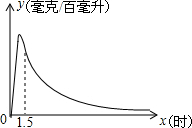 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(min) | 0 | 3 | 6 | 8 | 12 | … |
| y(m) | 5 | 70 | 5 | 54 | 5 | … |

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com