
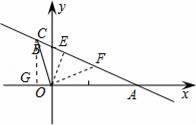
如图,在以点O为原点的直角坐标系中,一次函数y=﹣
 x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=
x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=
 AB,反比例函数y=
AB,反比例函数y=
 的图象经过点C,则k的值为 .
的图象经过点C,则k的值为 .


﹣
 .
.
【考点】反比例函数图象上点的坐标特征;一次函数图象上点的坐标特征.
【分析】首先求出点A、B的坐标,然后由勾股定理求得AB,设∠BAO=θ,则sinθ=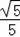
 ,cosθ=
,cosθ=
 ,过点O作RT△AOB斜边上的高OE,斜边上的中线OF,通过解直角三角形求得AE=OA•cosθ=2×
,过点O作RT△AOB斜边上的高OE,斜边上的中线OF,通过解直角三角形求得AE=OA•cosθ=2×
 =
=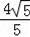
 ,根据三角形中线的性质求得OF=
,根据三角形中线的性质求得OF=
 AB,从而求得OC=OF=
AB,从而求得OC=OF=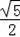
 ,进而求得AC=AE+EC=
,进而求得AC=AE+EC=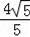
 +
+
 =
=
 .过点C作CG⊥x轴于点G,则CG=AC•sinθ=
.过点C作CG⊥x轴于点G,则CG=AC•sinθ=
 ×
×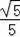
 =
=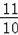
 ,AG=AC•cosθ=
,AG=AC•cosθ=
 ×
×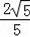
 =
=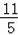
 ,从而求得C的坐标,然后根据待定系数法即可求得.
,从而求得C的坐标,然后根据待定系数法即可求得.
【解答】解:如图,在y=﹣
 x+1中,令y=0,则x=2;令x=0,得y=1,
x+1中,令y=0,则x=2;令x=0,得y=1,
∴A(2,0),B(0,1).
在Rt△AOB中,由勾股定理得:AB=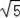
 .
.
设∠BAO=θ,则sinθ=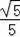
 ,cosθ=
,cosθ=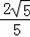
 .
.
过点O作RT△AOB斜边上的高OE,斜边上的中线OF,则AE=OA•cosθ=2×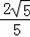
 =
=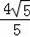
 ,OF=
,OF=
 AB,
AB,
∵OC=
 AB,
AB,
∴OC=OF=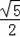
 ,
,
∴EF=AE﹣AF=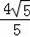
 ﹣
﹣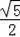
 =
=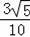
 .
.
∵OC=OF,OE⊥CF,
∴EC=EF=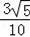
 ,
,
∴AC=AE+EC=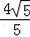
 +
+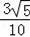
 =
=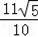
 .
.
过点C作CG⊥x轴于点G,则CG=AC•sinθ=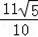
 ×
×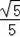
 =
=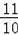
 ,
,
AG=AC•cosθ=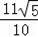
 ×
×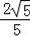
 =
=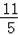
 ,
,
∴OG=AG﹣OA=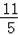
 ﹣2=
﹣2=
 .
.
∴C(﹣
 ,
,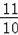
 ).
).
∵反比例函数y=
 的图象经过点C,
的图象经过点C,
∴k=﹣
 ×
×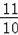
 =﹣
=﹣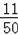
 ,
,
故答案为﹣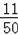
 .
.

【点评】本题考查了反比例函数与一次函数的交点问题,其知识点:勾股定理的应用,解直角三角形,直角三角形斜边中线的性质,待定系数法求解析式等.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
下列说法中,正确的是( )
A.为检测我市正在销售的酸奶质量,应该采用抽样调查的方式
B.两名同学连续五次数学测试的平均分相同,方差较大的同学数学成绩更稳定
C.抛掷一个正方体骰子,点数为奇数的概率是

D.“打开电视,正在播放广告”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
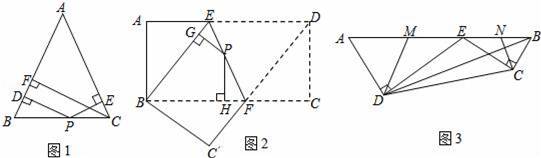
【问题情境】如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
【结论运用】如图2,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图3是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,
ED⊥AD,EC⊥CB,垂足分别为D、C,且AD•CE=DE•BC,AB=8,AD=3,BD=7;M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平行四边形ABCD中,点E是边AD的中点,连接EC交对角线BD于点F,则S△DEF:S△BCF等于( )
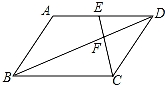
A.1:2 B.1:4 C.1:9 D.4:9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com