
【题目】如图,在![]() 中,延长
中,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,且
,且![]() .
.

(1)求证:![]() ;
;
(2)如果![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)详见解析;(2)40°
【解析】
(1)先由HL判定Rt△BCE≌Rt△CDF,得到∠ABC=∠DCF,然后由对顶角相等可得:∠DCF=∠ACB,进而可得∠ABC=∠ACB,然后由等角对等边,可得AB=AC;
(2)由CD=BC,可得∠CBD=∠CDB,然后由三角形的外角的性质可得:∠ACB=∠CBD+∠CDB=2∠CBD,由∠ABC=∠ACB,进而可得:∠ABC=2∠CBD,然后由∠ABD=∠ABC+∠CBD=3∠CBD=105![]() ,进而可求:∠CBD的度数及∠ABC的度数,然后由三角形的内角和定理即可求∠A的度数.
,进而可求:∠CBD的度数及∠ABC的度数,然后由三角形的内角和定理即可求∠A的度数.
解:(1)证明:∵![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读材料(1),并利用(1)的结论解决问题(2)和问题(3).
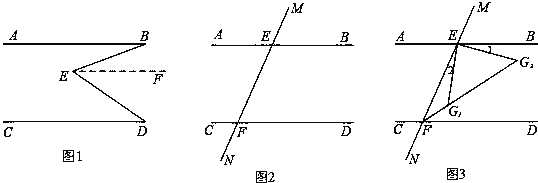
(1)如图1,AB∥CD,E为形内一点,连结BE、DE得到∠BED,求证:∠E=∠B+∠D
悦悦是这样做的:
过点E作EF∥AB.则有∠BEF=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
∴∠BEF+∠FED=∠B+∠D.
即∠BED=∠B+∠D.
(2)如图2,画出∠BEF和∠EFD的平分线,两线交于点G,猜想∠G的度数,并证明你的猜想.
(3)如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2,求证:∠FG1E+∠G2=180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
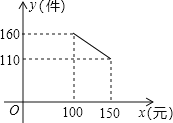
【题目】为发展“低碳经济”,某单位花12500引进了一条环保型生产线生产新产品,在生产过程中,每件产品还需成本40元,物价部门规定该产品售价不得低于100元/件且不得高于150元/件,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一个月该单位是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一个月盈利最大或亏损最小时,第二个月公司重新确定产品售价,能否使两个月共盈利达10800元?若能,求出第二个月的产品售价;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形![]() 的底边
的底边![]() 长为
长为![]() ,面积是
,面积是![]() , 腰
, 腰![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 边于
边于![]() 点.若点
点.若点![]() 为
为![]() 边的中点,点
边的中点,点![]() 为线段EF上一动点,则
为线段EF上一动点,则![]() 周长的最小值为( )
周长的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.
的中点.
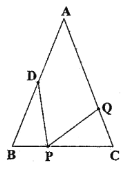
(1)如果点![]() 在线段
在线段![]() 上以
上以![]() 厘米
厘米![]() 秒的速度由
秒的速度由![]() 向
向![]() 点运动,同时点
点运动,同时点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动.
点运动.
①若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,
的运动速度相等,![]() 秒钟时,
秒钟时,![]() 与
与![]() 是否全等?请说明理由;
是否全等?请说明理由;
②点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() ?并说明理由;
?并说明理由;
(2)若点![]() 以②中的运动速度从点
以②中的运动速度从点![]() 出发,点
出发,点![]() 以原来运动速度从点
以原来运动速度从点![]() 同时出发,都逆时针沿
同时出发,都逆时针沿![]() 的三边运动,求多长时间点
的三边运动,求多长时间点![]() 与点
与点![]() 第一次在
第一次在![]() 的哪条边上相遇?
的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)观察图象,直接写出反比例函数值大于一次函数值x取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
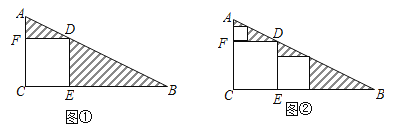
【题目】三角形纸片ABC中,∠C=90°,AC=1,BC=2.按图①的方式在这张纸片中剪去一个尽可能大的正方形,称为第1次剪取,记余下的两个三角形面积和为S1;按图②的方式在余下的Rt△ADF和Rt△BDE中,分别剪去尽可能大的正方形,称为第2次剪取,记余下的两个三角形面积和为S2;继续操作下去…….
(1)如图①,求![]() 和S1的值;
和S1的值;
(2)第n次剪取后,余下的所有三角形面积之和Sn为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户的养殖成本逐年增长,第一年的养殖成本为12万元,第3年的养殖成本为16万元.设养殖成本平均每年增长的百分率为x,则下面所列方程中正确的是( )
A. 12(1﹣x)2=16 B. 16(1﹣x)2=12 C. 16(1+x)2=12 D. 12(1+x)2=16
【答案】D
【解析】由题意可得:第二年的养殖成本为![]() ,
,
第三年的养殖成本为: ![]() ,
,
∴![]() .
.
故选D.
【题型】单选题
【结束】
8
【题目】一个布袋内只装有1个黑球和2个白球,这些球除颜色外其余都相同,随机摸出一个球后放回并搅匀,再随机摸出一个球,则两次摸出的球都是黑球的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com