
����Ŀ���������Ŀڴ���װ�зֱ���к��֡��������������������������������ĸ�С�����ֲ�֮ͬ�⣬С��û���κ�����ÿ������ǰ�Ƚ������������
��1����������ȡһ�������ϵĺ��ָպ��ǡ������ĸ���Ϊ���٣�
��2���״�����ȡһ���Żأ��ٴ�����ȡһ�����û���״ͼ�ķ����������ȡ�����������ϵĺ���ǡ����ɡ����������������ĸ���P1��
��3���Ҵ�����ȡһ���º��ֺ��ٷŻش��У��ٴ�����ȡһ����ȡ�����������ϵĺ���ǡ����ɡ����������������ĸ���ΪP2����Ƚ�P1��P2�Ĵ�С��ϵ��
���𰸡���1��![]() ��2����״ͼ�ԡ�
��2����״ͼ�ԡ�![]() (3)
(3)![]()
![]()
�������������������1����һ�������Ŀڴ���װ�зֱ���к��֡��������������������������������ĸ�С�����ֲ�֮ͬ�⣬С��û���κ�����ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
��2�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����ȡ�����������ϵĺ���ǡ����ɡ���������������������������ø��ʹ�ʽ������ô𰸣�
��3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����ȡ�����������ϵĺ���ǡ����ɡ���������������������������ø��ʹ�ʽ������ô𰸣�
�����������1����һ�������Ŀڴ���װ�зֱ���к��֡��������������������������������ĸ�С�����ֲ�֮ͬ�⣬С��û���κ�����
�������ȡһ�������ϵĺ��ָպ��ǡ��桱�ĸ���Ϊ��![]() ��
��
��2������״ͼ�ã�
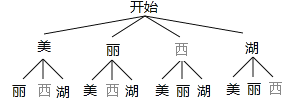
�߹���12�ֵȿ��ܵĽ����ȡ�����������ϵĺ���ǡ����ɡ������������������4�������
��P1=![]() ��
��
��3������״ͼ�ã�
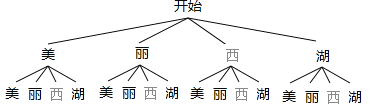
�߹���16�ֵȿ��ܵĽ����ȡ�����������ϵĺ���ǡ����ɡ������������������4�������
��P2=![]() ��
��
��P1��P2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���֪AB��8cm��BC��10cm���۵����ε�һ��AD �� ʹ��D����BC�ߵ��е�F�����ۺ�ΪAE �� ��CE�ij���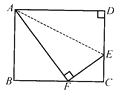
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ؿ�����ij���ӵ�·�峧������ɽ��ѧ��2014��Ӧ���ҵ������Ƹ��˾ְԱ����ӦƸ�ߵ�רҵ֪ʶ��Ӣ��ˮƽ���μ����ʵ�������Ż��������в��Ի�ɹ��϶�������ĵ÷����ֶ�Ϊ100�֣�����ķ����ֱ�5��3��2�ı�������ÿ�˵�����ܷ֣���4λӦƸ�ߵĵ÷������
�÷� | רҵ֪ʶ | Ӣ��ˮƽ | �μ����ʵ���� |
�� | 85 | 85 | 90 |
�� | 85 | 85 | 70 |
�� | 80 | 90 | 70 |
�� | 90 | 90 | 50 |
��1���ֱ����4λӦƸ�ߵ��ܷ֣�
��2���������ˡ�רҵ֪ʶ����ƽ����Ϊ85�֣�����Ϊ12.5�����ˡ�Ӣ��ˮƽ����ƽ����Ϊ87.5�֣�����Ϊ6.25������������ˡ��μ����ʵ�������Ż�ȡ���ƽ���ּ����
��3��������1���ͣ�2���е��й����ݣ���Դ�ѧ��ӦƸ���кν��飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P( x, y1)��Q (x, y2)�ֱ�����������ͼ��C1��C2�ϵ���һ��. ��a �� x �� bʱ����-1 �� y1 - y2 �� 1���������������������a �� x �� b���ǡ����ں������������������a �� x �� b���ǡ������ں�����.

���磬��P(x, y1)��Q (x, y2)�ֱ�����������y = 3x+1��y = 2x - 1ͼ���ϵ���һ�㣬��-3 �� x �� -1ʱ��y1 - y2 = (3x + 1) - (2x - 1) = x + 2��ͨ�����캯��y = x + 2���о��ú�����-3 �� x �� -1�ϵ����ʣ��õ��ú���ֵ�ķ�Χ��-1 �� y �� 1������-1 �� y1 - y2 �� 1���������������������-3 �� x �� -1���ǡ����ں�����.
��1���жϺ���y = 3x + 2��y = 2x + 1�ڣ�2 �� x�� 0���Ƿ�Ϊ�����ں�������˵�����ɣ�
��2��������y = x2 - x��y = x - a��0 �� x �� 2���ǡ����ں���������a��ȡֵ��Χ��
��3��������y =![]() ��y =��2x + 4��1 �� x �� 2���ǡ����ں�������ֱ��д��a�����ֵ����Сֵ.
��y =��2x + 4��1 �� x �� 2���ǡ����ں�������ֱ��д��a�����ֵ����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��AD��BC��D��EF��BC��F����3=��E����֤��ADƽ�֡�BAC�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ��ȥ����ֲ��10Ķ�ص��Ϲϣ�Ķ����Ϊ2000kg�������г���Ҫ�������ũ����������ֲ���������ȫ����ֲ�˸߲�����Ʒ���Ϲϣ���֪�Ϲ���ֲ�������������Ķ�����������ʵ�2���������Ϲϵ��ܲ���Ϊ60000kg�����Ϲ�Ķ�����������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
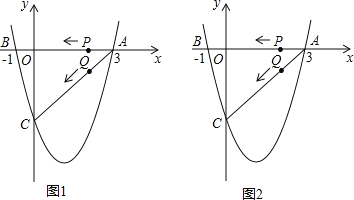
����Ŀ����ͼ1��ע����ͼ2��ȫ��ͬ�������κ���y=![]() x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y�ύ�ڵ�C��
x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y�ύ�ڵ�C��
��1����ö��κ����Ľ���ʽ��
��2����������ߵĶ���ΪD������ACD�������
��3������P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶�����P��Q�˶���t��ʱ����APQ��PQ���ڵ�ֱ�߷��ۣ���Aǡ��������������E�㴦����ֱ���ж���ʱ�ı���APEQ����״�������E������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������������֤����ABC�ա�DCB���ǣ� �� 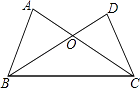
A.AB=DC��AC=DB
B.AB=DC����ABC=��DCB
C.BO=CO����A=��D
D.AB=DC����A=��D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��m+3��m+1����ֱ������ϵ��x���ϣ���P�������Ϊ�� ��
A.��0����2��
B.��2��0��
C.��0��2��
D.��0����4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com