
【题目】已知点![]() 在直线
在直线![]() 上,
上,
(1)直线![]() 解析式为 ;
解析式为 ;
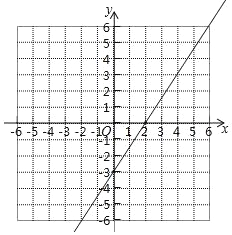
(2)画出该一次函数的图象;
(3)将直线![]() 向上平移
向上平移![]() 个单位长度得到直线
个单位长度得到直线![]() ,
,![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标为 ;
的坐标为 ;
(4)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,![]() 点坐标为 ;
点坐标为 ;
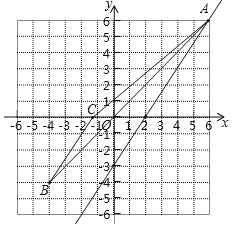
(5)三角形ABC的面积为 ;
(6)由图象可知不等式![]() 的解集为 .
的解集为 .

【答案】(1)![]() ;(2)图象见解析;(3)
;(2)图象见解析;(3)![]() ;(4)
;(4)![]() ;(5)
;(5)![]() ;(6)
;(6)![]() .
.
【解析】
(1)根据点![]() 在直线
在直线![]() 上,把点A代入解析式即可求解;
上,把点A代入解析式即可求解;
(2) 令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ,据此可求得函数图像;
,据此可求得函数图像;
(3)根据平移规律可得![]() 的解析式为
的解析式为![]() ,进而得到
,进而得到![]() ;
;
(4) 解方程组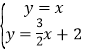 ,可得
,可得![]() ;进而得到
;进而得到![]() ;
;
(5) 由![]() ,
,![]() ,
,![]() ,可得
,可得![]() ;
;
(6)由图像可知不等式![]() 的解集.
的解集.
解:(1)![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,即
,即![]() ,
,
![]() 直线
直线![]() 解析式为:
解析式为:![]() ;
;
故答案为:![]() ;
;
(2)令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ;
;
函数图象如图:
(3)将直线![]() 向上平移
向上平移![]() 个单位长度得到直线
个单位长度得到直线![]() ,则
,则![]() 的解析式为
的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
解得![]() ,
,
![]() ;
;
故答案为:![]() ;
;
(4)由题可得,直线![]() 的解析式为
的解析式为![]() ,
,
解方程组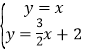 ,可得
,可得![]() ,
,
![]() ;
;
故答案为:![]() ;
;
(5)由![]() ,
,![]() ,
,![]() ,可得
,可得
![]() ;
;
故答案为:![]() ;
;
(6)由图象可知不等式![]() 的解集为:
的解集为:![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
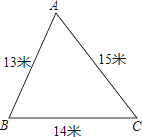
【题目】学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为60元,学校修建这个花园需要投资多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为16cm2,对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( )

A. ![]() cm2 B. 1cm2 C. 2cm2 D. 4cm2
cm2 B. 1cm2 C. 2cm2 D. 4cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示则①abc<0;②a﹣b+c<0;③3a+c<0;④当﹣1<x<3时,y>0.其中判断正确的有( )个. 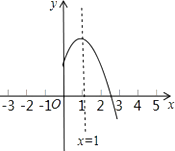
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,两正方形在数轴上运动,起始状态如图所示.A、F表示的数分别为-2、10,大正方形的边长为4个单位长度,小正方形的边长为2个单位长度,两正方形同时出发,相向而行,小正方形的速度是大正方形速度的两倍,两个正方形从相遇到刚好完全离开用时2秒.完成下列问题:
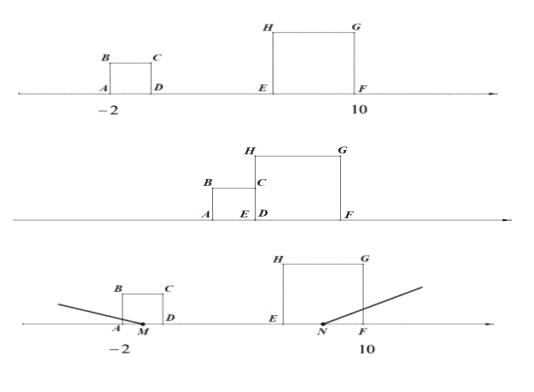
(1)求起始位置D、E表示的数;
(2)求两正方形运动的速度;
(3)M、N分别是AD、EF中点,当正方形开始运动时,射线MA开始以15°/s的速度顺时针旋转至MD结束,射线NF开始以30°/s的速度逆时针旋转至NE结束,若两射线所在直线互相垂直时,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1: ![]() ,求旗杆AB的高度(
,求旗杆AB的高度( ![]() ,结果精确到个位).
,结果精确到个位).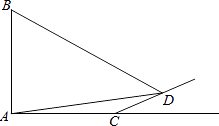
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.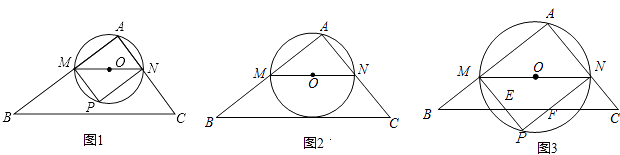
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切;
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格纸中,小正方形的顶点叫做格点,△ABC是一个格点三角形(即△ABC的三个顶点都在格点上),根据要求回答下列问题:

(1)画出△ABC先向左平移6格,再向上平移1格所得的△A′B′C′;
(2)利用网格画出△ABC中BC边上的高AD.
(3)过点A画直线l,将△ABC分成面积相等的两个三角形;
(4)在直线AB的右侧格点图中标出所有格点E(不包括点C),使S△ABE=S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°, BC=12cm,半圆O以 2cm/s 的速度从左向右运动,在运动过程中,点 D 、E 始终在直线BC 上.设运动时间为t(s) ,当t=0s时,半圆O在△ABC的左侧,OC=8cm。
(1)当t =(s)时,⊙O与AC所在直线第一次相切,点 C 到直线 AB 的距离为;
(2)当 t为何值时,直线 AB 与半圆O所在的圆相切;
(3)当△ABC的一边所在直线与圆O相切时,若⊙O与△ABC有重叠部分,求重叠部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com