Question

【题目】如图，旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处，某校数学课外兴趣小组的同学正在测量旗杆的高度，在旗杆的底部A处测得点D的仰角为15°，AC=10米，又测得∠BDA=45°．已知斜坡CD的坡度为i=1： ，求旗杆AB的高度（ ，结果精确到个位）．

Answer 1

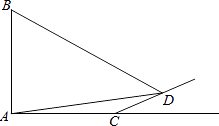
【答案】解：延长BD，AC交于点E，过点D作DF⊥AE于点F．

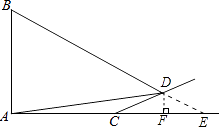
∵i=tan∠DCF= = ，

∴∠DCF=30°．

又∵∠DAC=15°，

∴∠ADC=15°．

∴CD=AC=10．

在Rt△DCF中，DF=CDsin30°=10× =5（米），

CF=CDcos30°=10× =5 ，∠CDF=60°．

∴∠BDF=45°+15°+60°=120°，

∴∠E=120°﹣90°=30°，

在Rt△DFE中，EF= = =5

∴AE=10+5 +5 =10 +10．

在Rt△BAE中，BA=AEtanE=（10 +10）× =10+ ≈16（米）．

答：旗杆AB的高度约为16米．

【解析】根据解直角三角形中斜坡CD的坡度为i，由特殊角的三角函数值，得到∠DCF=30°；求出DF=CDsin30°、CF=CDcos30°的值，得到AE的值，在Rt△BAE中，求出BA=AEtanE的值.
【考点精析】关于本题考查的关于仰角俯角问题，需要了解仰角：视线在水平线上方的角；俯角：视线在水平线下方的角才能得出正确答案．