
【题目】已知,两正方形在数轴上运动,起始状态如图所示.A、F表示的数分别为-2、10,大正方形的边长为4个单位长度,小正方形的边长为2个单位长度,两正方形同时出发,相向而行,小正方形的速度是大正方形速度的两倍,两个正方形从相遇到刚好完全离开用时2秒.完成下列问题:
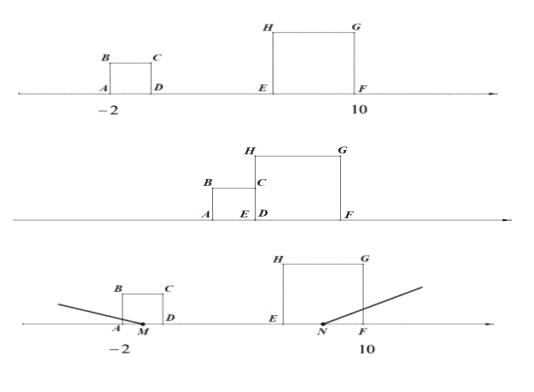
(1)求起始位置D、E表示的数;
(2)求两正方形运动的速度;
(3)M、N分别是AD、EF中点,当正方形开始运动时,射线MA开始以15°/s的速度顺时针旋转至MD结束,射线NF开始以30°/s的速度逆时针旋转至NE结束,若两射线所在直线互相垂直时,求MN的长.
【答案】(1)0,6;(2)小正方形速度2个单位/秒,大正方形速度1个单位/秒;(3)t=2, MN=3,t=6, MN=9
【解析】
(1)利用图象和正方形的边长即可得出;
(2)设小正方形的速度是2x个单位/秒,大正方形的速度是x个单位/秒,然后列方程计算即可;
(3)由题意可得若想要两射线所在直线互相垂直,则有①15°t+30°t=90°或②15°t+30°t=270°
两种情况,根据两种情况分别讨论即可.
(1)∵A、F表示的数分别为-2、10,大正方形的边长为4个单位长度,小正方形的边长为2个单位长度,
∴D表示的数为:-2+2=0,E表示的数为:10-4=6;
(2)解:设小正方形的速度是2x个单位/秒,大正方形的速度是x个单位/秒,
则有2(2x+x)=2+4,
解得:x=1,
∴小正方形的速度是2个单位/秒,
故小正方形速度2个单位/秒,大正方形速度1个单位/秒;
(3)设运动时间为t,
由题意可得若想要两射线所在直线互相垂直,
则有①15°t+30°t=90°或②15°t+30°t=270°,
①15°t+30°t=90°,解得t=2,
此时小正方形运动了4个单位,D点在数字4的位置,大正方形运动了2个单位,E点也在数字4的位置,即D,E重合,
∵M、N分别是AD、EF中点,
∴MN=3;
②15°t+30°t=270°,解得t=6,
此时小正方形运动了12个单位,D点在数字12的位置,大正方形运动了6个单位,E点在数字0的位置,
∵M、N分别是AD、EF中点,
∴此时M点位于数字11的位置,N点位于数字2的位置,
∴MN=11-2=9;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4cm,AD=6cm,延长AB到E,使BE=2AB,连接CE,动点F从A出发以2cm/s的速度沿AE方向向点E运动,动点G从E点出发,以3cm/s的速度沿E→C→D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止,设动点运动的时间为t秒.
(1)当t为何值时,FC与EG互相平分;
(2)连接FG,当t< ![]() 时,是否存在时间t使△EFG与△EBC相似?若存在,求出t的值;若不存在,请说明理由.
时,是否存在时间t使△EFG与△EBC相似?若存在,求出t的值;若不存在,请说明理由.
(3)设△EFG的面积为y,求出y与t的函数关系式,求当t为何值时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:以O为圆心的扇形AOB中,∠AOB=90°,点C为 ![]() 上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.
上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.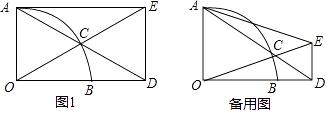
(1)如图1,当四边形AODE为矩形时,求∠ADO的度数;
(2)当扇形的半径长为5,且AC=6时,求线段DE的长;
(3)联结BC,试问:在点C运动的过程中,∠BCD的大小是否确定?若是,请求出它的度数;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备购买A、B两种零件,已知A种零件的单价比B种零件的单价多30元,而用900元购买A种零件的数量和用600元购买B种零件的数量相等.
(1)求A、B两种零件的单价;
(2)根据需要,工厂准备购买A、B两种零件共200件,工厂购买两种零件的总费用不超过14700元,求工厂最多购买A种零件多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在直线
在直线![]() 上,
上,
(1)直线![]() 解析式为 ;
解析式为 ;
(2)画出该一次函数的图象;
(3)将直线![]() 向上平移
向上平移![]() 个单位长度得到直线
个单位长度得到直线![]() ,
,![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标为 ;
的坐标为 ;
(4)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,![]() 点坐标为 ;
点坐标为 ;
(5)三角形ABC的面积为 ;
(6)由图象可知不等式![]() 的解集为 .
的解集为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2= ![]() 的图象相交于A,B两点,点B的坐标为(2m,﹣m).
的图象相交于A,B两点,点B的坐标为(2m,﹣m).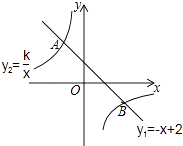
(1)求出m值并确定反比例函数的表达式;
(2)请直接写出当x<m时,y2的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y1= ![]() (a>0,a为常数)和y2=
(a>0,a为常数)和y2= ![]() 在第一象限内的图象如图所示,点M在y2=
在第一象限内的图象如图所示,点M在y2= ![]() 的图象上,MC⊥x轴于点C,交y1=
的图象上,MC⊥x轴于点C,交y1= ![]() 的图象于点A;MD⊥y轴于点D,交y1=
的图象于点A;MD⊥y轴于点D,交y1= ![]() 的图象于点B,当点M在y2=
的图象于点B,当点M在y2= ![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积为2﹣a;
③当a=1时,点A是MC的中点;
④若S四边形OAMB=S△ODB+S△OCA , 则四边形OCMD为正方形.
其中正确的是 . (把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】福田区某轿车销售公司为龙泉工业区代销 A 款轿车,为了吸引购车族,销售公司打出降价牌,今年 5月份A款轿车每辆售价比去年同期每辆售价低 1万元,如果卖出相同数量的 A 款轿车,去年的销售额为100万元,今年销售额只有90万元.
(1)今年 5月份 A 款轿车每辆售价为多少元?
(2)为了增加收入,该轿车公司决定再为龙泉工业区代销 B款轿车,已知 A款轿车每辆进价为 7.5万元,B款轿车每辆进价为 6万元,公司预计用不多于105万元的资金购进这两款轿车共 15 辆,但A款轿车不多于6辆,试问共有几种进货方案?
(3)在⑵的条件下,B款轿车每辆售价为 8万元,为打开B款轿车的销路,公司决定每售出一辆 B款轿车,返还顾客现金a( 0<a ≤1 )万元.假设购进的15辆车能够全部卖出去,试讨论采用哪种进货方案可以使该轿车销售公司卖出这 15辆车后获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com