
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2= ![]() 的图象相交于A,B两点,点B的坐标为(2m,﹣m).
的图象相交于A,B两点,点B的坐标为(2m,﹣m).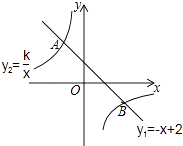
(1)求出m值并确定反比例函数的表达式;
(2)请直接写出当x<m时,y2的取值范围.
科目:初中数学 来源: 题型:
【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,两正方形在数轴上运动,起始状态如图所示.A、F表示的数分别为-2、10,大正方形的边长为4个单位长度,小正方形的边长为2个单位长度,两正方形同时出发,相向而行,小正方形的速度是大正方形速度的两倍,两个正方形从相遇到刚好完全离开用时2秒.完成下列问题:
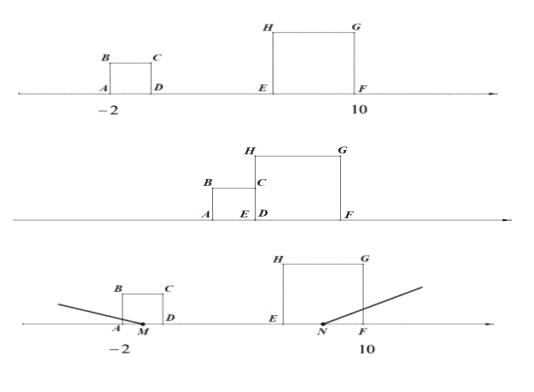
(1)求起始位置D、E表示的数;
(2)求两正方形运动的速度;
(3)M、N分别是AD、EF中点,当正方形开始运动时,射线MA开始以15°/s的速度顺时针旋转至MD结束,射线NF开始以30°/s的速度逆时针旋转至NE结束,若两射线所在直线互相垂直时,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , …按这样的规律进行下去,第2017个正方形的面积为 . 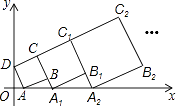
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.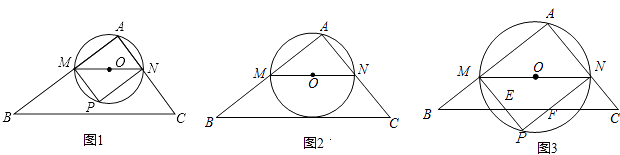
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切;
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得△A1B1C1 , 且点A1落在边AB边上,取BB1的中点D,连接CD,则CD的长为( )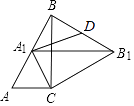
A.![]()
B.![]()
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:

(习题回顾)已知:如图1,在![]() 中,
中,![]() ,
,![]() 是角平分线,
是角平分线,![]() 是高,
是高,![]() 、
、![]() 相交于点
相交于点![]() .求证:
.求证:![]() ;
;
(变式思考)如图2,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的高,若
边上的高,若![]() 的外角
的外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() ,其反向延长线与
,其反向延长线与![]() 边的延长线交于点
边的延长线交于点![]() ,则
,则![]() 与
与![]() 还相等吗?说明理由;
还相等吗?说明理由;
(探究延伸)如图3,在![]() 中,
中,![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() .
.![]() 的外角
的外角![]() 的平分线所在直线
的平分线所在直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .直接写出
.直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买一个乙种书柜比购买一个甲种书柜贵60元,若购买甲种书柜1个、乙种书柜2个,共需资金660元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请问学校有哪几种购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com