
【题目】如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°, BC=12cm,半圆O以 2cm/s 的速度从左向右运动,在运动过程中,点 D 、E 始终在直线BC 上.设运动时间为t(s) ,当t=0s时,半圆O在△ABC的左侧,OC=8cm。
(1)当t =(s)时,⊙O与AC所在直线第一次相切,点 C 到直线 AB 的距离为;
(2)当 t为何值时,直线 AB 与半圆O所在的圆相切;
(3)当△ABC的一边所在直线与圆O相切时,若⊙O与△ABC有重叠部分,求重叠部分的面积.
【答案】
(1)1.,6.
(2)解:如图2: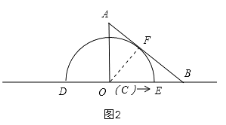
过点C作CF⊥AB于点F,
∴OF=6,
当直线AB于半圆O所在的圆相切时,
∵圆心O到AB的距离为6,半圆的半径为6,且圆心O又在BC上,
∴点O与点C重合,
即当点O运动到点C时,半圆O与![]() ABC的边AB相切,此时点O运动了8cm,t=8
ABC的边AB相切,此时点O运动了8cm,t=8![]() 2=4,
2=4,
如图3: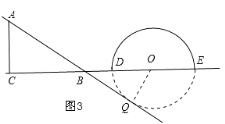
当点O运动到点B的右侧时,且OB=12 ,
过点O作OQ⊥AB于点Q,
在Rt![]() OQB中,∠OBQ=30°,则OQ=
OQB中,∠OBQ=30°,则OQ=![]() OB=6,
OB=6,
即OQ与半圆O所在的圆相切,此时点O运动了12+12+8=32cm,t=32![]() 2=16,
2=16,
综上,当t为4秒或6秒时,直线 AB 与半圆O所在的圆相切.
(3)解:①当半圆O与AB边相切于点F时,如图2: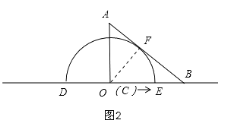
重叠部分的面积S=![]() 62=9
62=9![]() ;
;
②当半圆O与AC相切与点C时,如图4: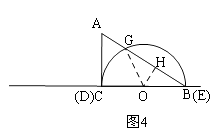
连接OG,
∵BC=DE=12,
∴点C与点D重合,点E与点B重合,
∵OG=OB,
∴∠ABC=∠OGB=30°,
∴∠COG=60°,
过点O作OH⊥AB于点H,
∵OB=6,
∴OH=![]() OB=3,
OB=3,
∴BH=![]() ,
,
∴BG=2BH=![]() ,
,
此时重叠部分的面积S=![]() =
=![]() ;
;
综上,重叠部分的面积为9![]() cm2或(
cm2或(![]() )cm2.
)cm2.
【解析】解:(1)∵DE=12,
∴OE=OD=6,
∵OC=8,
∴EC=8-6=2,
∴t=2![]() 2=1,
2=1,
∴当t=1时,⊙O与AC所在直线第一次相切;
如图1,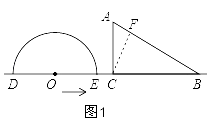
过点C作CF⊥AB于F,
在Rt![]() BCF中,∵∠ABC=30°,BC=12,
BCF中,∵∠ABC=30°,BC=12,
∴CF=![]() BC=6,
BC=6,
所以答案是:1,6.
【考点精析】利用勾股定理的概念对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】已知点![]() 在直线
在直线![]() 上,
上,
(1)直线![]() 解析式为 ;
解析式为 ;
(2)画出该一次函数的图象;
(3)将直线![]() 向上平移
向上平移![]() 个单位长度得到直线
个单位长度得到直线![]() ,
,![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标为 ;
的坐标为 ;
(4)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,![]() 点坐标为 ;
点坐标为 ;
(5)三角形ABC的面积为 ;
(6)由图象可知不等式![]() 的解集为 .
的解集为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A,C分别在x轴,y轴的正半轴上,抛物线L经过O,P,A三点,点E是正方形内的抛物线上的动点.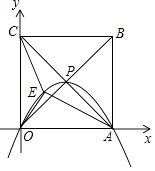
(1)点P的坐标为;
(2)求抛物线L的解析式;
(3)求△OAE与△OCE面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感恩是中华民族的传统美德,在4月份某校提出了“感恩父母、感恩老师、感恩他人”的“三感”教育活动.感恩事例有:A.给父母过一次生日;B .为父母做一次家务活,让父母休息一天;C.给老师一个发自内心的拥抱,并且与老师谈心;D.帮助有困难的同学度过难关.为了解学生对这四种感恩事例的情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学在4种感恩事例中选择最想做的一种),将数据进行整理并绘制成以下两幅统计图(未画完整).
(1)这次调查中,一共查了名学生;
(2)请补全扇形统计图中的数据及条形统计图;
(3)若有3名选 A的学生,1名选 C的学生组成志愿服务队外出参加联谊活动,欲从中随机选出2人担任活动负责人,请通过树状图或列表求两人均是选 A的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】福田区某轿车销售公司为龙泉工业区代销 A 款轿车,为了吸引购车族,销售公司打出降价牌,今年 5月份A款轿车每辆售价比去年同期每辆售价低 1万元,如果卖出相同数量的 A 款轿车,去年的销售额为100万元,今年销售额只有90万元.
(1)今年 5月份 A 款轿车每辆售价为多少元?
(2)为了增加收入,该轿车公司决定再为龙泉工业区代销 B款轿车,已知 A款轿车每辆进价为 7.5万元,B款轿车每辆进价为 6万元,公司预计用不多于105万元的资金购进这两款轿车共 15 辆,但A款轿车不多于6辆,试问共有几种进货方案?
(3)在⑵的条件下,B款轿车每辆售价为 8万元,为打开B款轿车的销路,公司决定每售出一辆 B款轿车,返还顾客现金a( 0<a ≤1 )万元.假设购进的15辆车能够全部卖出去,试讨论采用哪种进货方案可以使该轿车销售公司卖出这 15辆车后获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你用学习“一次函数”时积累的经验和方法研究函数![]() 的图象和性质,并解决问题.
的图象和性质,并解决问题.
![]() 完成下列步骤,画出函数
完成下列步骤,画出函数![]() 的图象;
的图象;
![]() 列表、填空;
列表、填空;
x |
|
|
|
| 0 | 1 | 2 | 3 |
|
y |
| 3 | ______ | 1 | ______ | 1 | 2 | 3 |
|
![]() 描点:
描点:
![]() 连线
连线
![]() 观察图象,当x______时,y随x的增大而增大;
观察图象,当x______时,y随x的增大而增大;
![]() 结合图象,不等式
结合图象,不等式![]() 的解集为______.
的解集为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,M,N分别是边AB、BC的中点,E、F是边AC上的三等分点,连接ME、NF且延长后交于点D,连接BE、BF
(1)求证:四边形BFDE是平行四边形;(2)当△ABC满足什么条件时四边形BFDE是菱形,证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线PQ∥MN,点C是PQ、MN之间(不在直线PQ,MN上)的一个动点.

(1)若∠1与∠2都是锐角,如图甲,请直接写出∠C与∠1,∠2之间的数量关系;
(2)若把一块三角尺(∠A=30°,∠C=90°)按如图乙方式放置,点D,E,F是三角尺的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数;
(3)将图乙中的三角尺进行适当转动,如图丙,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,且有∠CEG=∠CEM,求![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com