
【题目】如图,直线PQ∥MN,点C是PQ、MN之间(不在直线PQ,MN上)的一个动点.

(1)若∠1与∠2都是锐角,如图甲,请直接写出∠C与∠1,∠2之间的数量关系;
(2)若把一块三角尺(∠A=30°,∠C=90°)按如图乙方式放置,点D,E,F是三角尺的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数;
(3)将图乙中的三角尺进行适当转动,如图丙,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,且有∠CEG=∠CEM,求![]() 值.
值.
【答案】(1)∠C=∠1+∠2,理由见解析;(2)60°;(3)2
【解析】
(1)过C作CD∥PQ,依据平行线的性质,即可得出∠C=∠1+∠2;
(2)根据(1)中的结论可得,∠C=∠MEC+∠PDC=90°,再根据对顶角相等即可得出结论;
(3)设∠CEG=∠CEM=x,得到∠GEN=180°2x,再根据(1)中的结论可得∠CDP=90°∠CEM=90°x,再根据对顶角相等即可得出∠BDF=90°x,据此可得![]() 的值.
的值.
(1)∠C=∠1+∠2.
理由:如图,过C作CD∥PQ,
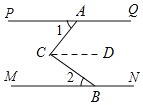
∵PQ∥MN,
∴PQ∥CD∥MN,
∴∠1=∠ACD,∠2=∠BCD,
∴∠ACB=∠ACD+∠BCD=∠1+∠2.
(2)∵∠AEN=∠A=30°,
∴∠MEC=30°,
由(1)可得,∠C=∠MEC+∠PDC=90°,
∴∠PDC=90°﹣∠MEC=60°,
∴∠BDF=∠PDC=60°;
(3)设∠CEG=∠CEM=x,则∠GEN=180°﹣2x,
由(1)可得,∠C=∠CEM+∠CDP,
∴∠CDP=90°﹣∠CEM=90°﹣x,
∴∠BDF=90°﹣x,
∴![]() =
=![]() =2.
=2.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°, BC=12cm,半圆O以 2cm/s 的速度从左向右运动,在运动过程中,点 D 、E 始终在直线BC 上.设运动时间为t(s) ,当t=0s时,半圆O在△ABC的左侧,OC=8cm。
(1)当t =(s)时,⊙O与AC所在直线第一次相切,点 C 到直线 AB 的距离为;
(2)当 t为何值时,直线 AB 与半圆O所在的圆相切;
(3)当△ABC的一边所在直线与圆O相切时,若⊙O与△ABC有重叠部分,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:

(1)根据图中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1: ;
方法2: .
(2)从中你能发现什么结论,请用等式表示出来: ;
(3)利用(2)中结论解决下面的问题:若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数 ![]() (x>0)的图象经过点D.已知S△BCE=2,则k的值是( )
(x>0)的图象经过点D.已知S△BCE=2,则k的值是( )
A.2
B.﹣2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y= ![]() (k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n,
(k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n, ![]() ),过点E的直线l交x轴于点F,交y轴于点G(0,﹣2),则点F的坐标是 .
),过点E的直线l交x轴于点F,交y轴于点G(0,﹣2),则点F的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象.根据图象提供的信息,解答下列问题: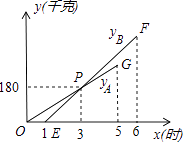
(1)求yB关于x的函数解析式;
(2)如果A、B两种机器人连续搬运5个小时,那么B种机器人比A种机器人多搬运了多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家![]() 妈妈8:30从家出发,乘车沿相同路线去姥姥家
妈妈8:30从家出发,乘车沿相同路线去姥姥家![]() 在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是
在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是![]()
![]()

A. 9:00妈妈追上小亮B. 妈妈比小亮提前到达姥姥家
C. 小亮骑自行车的平均速度是![]() D. 妈妈在距家13km处追上小亮
D. 妈妈在距家13km处追上小亮
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
⑴ac<0;
⑵当x>1时,y的值随x值的增大而减小.
⑶3是方程ax2+(b﹣1)x+c=0的一个根;
⑷当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com