
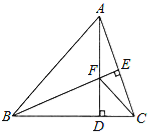
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
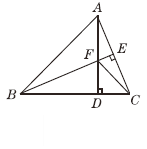
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
【答案】(2)2+![]()
【解析】试题分析:(1)先判定出△ABD是等腰直角三角形,根据等腰直角三角形的性质可得AD=BD,再根据同角的余角相等求出∠CAD=∠CBE,然后利用“角边角”证明△ADC和△BDF全等,根据全等三角形对应边相等可得BF=AC,再根据等腰三角形三线合一的性质可得AC=2AE,从而得证;
(2)根据全等三角形对应边相等可得DF=CD,然后利用勾股定理列式求出CF,再根据线段垂直平分线上的点到线段两端点的距离相等可得AF=CF,然后根据AD=AF+DF代入数据即可得解.
(1)证明:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC
∴∠CAD+∠ACD=90°,
∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中,![]() ,
,
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
(2)解:∵△ADC≌△BDF,
∴DF=CD=,
在Rt△CDF中,CF=![]() =
=![]() =2,
=2,
∵BE⊥AC,AE=EC,
∴AF=CF=2,
∴AD=AF+DF=2+.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )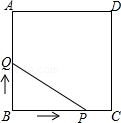
A.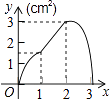
B.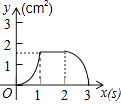
C.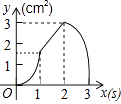
D.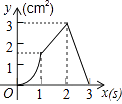
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,“回”字形的道路宽为1米,整个“回”字形的长为8米,宽为1米,一个人从入口点A沿着道路中央走到中点B,他共走了( )

A. 55米 B. 55.5米 C. 56米 D. 56.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>9且x<26,单位:km)

(1)说出这辆出租车每次行驶的方向.
(2)求经过连续4次行驶后,这辆出租车所在的位置.
(3)这辆出租车一共行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,三角形ABC是等边三角形,D是BC边上的一点,三角形ABD经过旋转后到达三角形ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M到了什么位置?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是( ).

A.AE∥BC B. ∠ADE=∠BDC
C.△BDE是等边三角形 D. △ADE的周长是9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com