
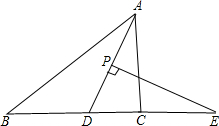
 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.分析 (1)先根据三角形的内角和定理求得∠BAC的度数,再根据角平分线的定义求得∠DAC的度数,从而根据三角形的内角和定理即可求出∠ADC的度数,进一步求得∠E的度数;
(2)根据第(1)小题的思路即可推导这些角之间的关系.
解答 解:(1)∵∠B=35°,∠ACB=85°,
∴∠BAC=60°,
∵AD平分∠BAC,
∴∠DAC=30°,
∴∠ADC=65°,
∴∠E=25°.
故答案为:25°;
(2)∠E=$\frac{β-α}{2}$.
∵AD平分∠BAC,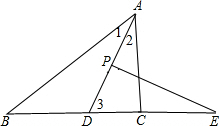
∴∠1=∠2=$\frac{1}{2}$∠BAC,
∵∠B+∠ACB+∠BAC=180°,
∵∠B=α,∠ACB=β,
∴∠CAB=180°-α-β,
∴∠BAD=$\frac{1}{2}$(180°-α-β),
∴∠3=∠B+∠1=α+$\frac{1}{2}$(180°-α-β)=90°+$\frac{1}{2}$α-$\frac{1}{2}$β,
∵PE⊥AD,
∴∠DPE=90°,
∴∠E=90°-(90°+$\frac{1}{2}$α-$\frac{1}{2}$β)=$\frac{1}{2}$(m-n)°=$\frac{1}{2}$(β-α).
故答案为:$\frac{β-α}{2}$.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.


科目:初中数学 来源: 题型:选择题
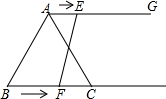 如图,在等边三角形ABC中,AB=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,当四边形AEFC是平行四边形时,运动时间t的值为( )
如图,在等边三角形ABC中,AB=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,当四边形AEFC是平行四边形时,运动时间t的值为( )| A. | 2s | B. | 6s | C. | 8s | D. | 2s或6s |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+2y)(x-2y) | B. | (a+b)(a-2b) | C. | (-a+2b)(a-2b) | D. | (-2m-n)(2m+n) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1 | 2 | 3 | 4 |
| 多项式 | 常数项 | 一次项系数 | 分解因式 |
| x2+6x+8 | 8=2×4 | 6=2+4 | x2+6x+8=(x+2)(x+4) |
| x2-6x+8 | 8=(-2)×(-4) | -6=(-2)+(-4) | x2-6x+8=(x-2)(x-4) |
| x2+2x-8 | -8=4×(-2) | 2=4+(-2) | x2+2x-8=(x+4)(x-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com