
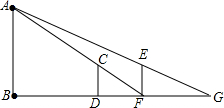
 如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小华在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小华的身高为1.5m,求路灯杆AB的高度.
如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小华在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小华的身高为1.5m,求路灯杆AB的高度. 分析 在同一时刻物高和影长成正比,根据相似三角形的性质即可解答.
解答  解:∵CD∥EF∥AB,
解:∵CD∥EF∥AB,
∴可以得到△CDF∽△ABF,△ABG∽△EFG,
∴$\frac{CD}{AB}$=$\frac{DF}{BF}$,$\frac{FE}{AB}$=$\frac{FG}{BG}$,
又∵CD=EF,
∴$\frac{DF}{BF}$=$\frac{FG}{BG}$,
∵DF=3m,FG=4m,BF=BD+DF=BD+3,BG=BD+DF+FG=BD+7,
∴$\frac{3}{DB+3}$=$\frac{4}{BD+7}$,
∴BD=9,BF=9+3=12,
∴$\frac{1.5}{AB}$=$\frac{3}{12}$,
解得AB=6.
答:路灯杆AB的高度是6m.
点评 本题考查了相似三角形的应用和中心投影.只要是把实际问题抽象到相似三角形中,利用相似三角形的性质对应边成比例就可以求出结果.


科目:初中数学 来源: 题型:选择题
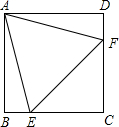 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEF=75°;③BE+DF=EF;④${S_{正方形ABCD}}=2+\sqrt{3}$;⑤$tan∠AEB=2+\sqrt{3}$,其中正确的( )个.
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEF=75°;③BE+DF=EF;④${S_{正方形ABCD}}=2+\sqrt{3}$;⑤$tan∠AEB=2+\sqrt{3}$,其中正确的( )个.| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
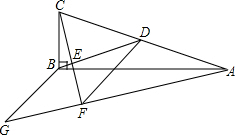 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点p是x轴上的一个动点,过点p作x轴的垂线,交双曲线$y=\frac{k}{x}(k≠0)$于点Q,连接OQ,当点p沿x轴的正半轴方向运动时,Rt△POQ的面积( )
如图,点p是x轴上的一个动点,过点p作x轴的垂线,交双曲线$y=\frac{k}{x}(k≠0)$于点Q,连接OQ,当点p沿x轴的正半轴方向运动时,Rt△POQ的面积( )| A. | 逐渐增大 | B. | 不变 | C. | 逐渐减小 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向左移动1个单位,向上移动3个单位 | |
| B. | 向右移动1个单位,向上移动3个单位 | |
| C. | 向左移动1个单位,向下移动3个单位 | |
| D. | 向右移动1个单位,向下移动3个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它是三次三项式 | B. | 它是四次两项式 | ||
| C. | 它的最高次项是-6x2yz | D. | 它的常数项是1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com