
【题目】如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() 于
于![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 延长线上一点,若
延长线上一点,若![]() ,则
,则![]() ________.
________.

【答案】![]()
【解析】
由于D是弧AC的中点,可知∠ABC=2∠ACD;由于半径AO⊥BC,由垂径定理易证得AB=AC,即∠ACB=∠ABC=2∠ACD,由圆内接四边形的性质知:∠BCD=∠DAE=120°,由此可求出∠ACD的度数;而∠DAC和∠DCA是等弧所对的圆周角,则∠DAC=∠DCA,由此得解.
∵AO⊥BC,且AO是⊙O的半径,
∴AO垂直平分BC,
∴AB=AC,即∠ABC=∠ACB,
∵D是![]() 的中点,
的中点,
∴∠ABC=2∠DCA=2∠DAC,
∴∠ACB=2∠DCA,
∵四边形ABCD内接于⊙O,
∴∠BCD=∠DAE=120°,
∴∠ACB+∠DCA=120°,
即3∠DCA=120°,
∴∠DAC=∠DCA=40°.
故答案为:40


科目:初中数学 来源: 题型:
【题目】阅读与思考:利用多项式的乘法法则,可以得到![]() ,反过来,则有
,反过来,则有![]() 利用这个式子可以将某些二次项系数是1的二次三项式分解因式。例如:将式子
利用这个式子可以将某些二次项系数是1的二次三项式分解因式。例如:将式子![]() 分解因式.这个式子的常数项
分解因式.这个式子的常数项![]() ,一次项系数
,一次项系数![]() ,所以
,所以![]() .
.
解:![]() .
.
上述分解因式![]() 的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图).
的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图).
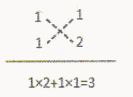
请仿照上面的方法,解答下列问题:
(1)分解因式:![]() ;
;
(2)分解因式:![]() ;
;
(3)若![]() 可分解为两个一次因式的积,写出整数P的所有可能值.
可分解为两个一次因式的积,写出整数P的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=40°,点D在BC边上(不与C、D点重合),点P、点Q分别是AC、AB边上的动点,当△DPQ的周长最小时,则∠PDQ的度数为( )

A. 140°B. 120°C. 100°D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级三班学生苏琪为帮助同桌万宇巩固“平面直角坐标系四个象限内及坐标轴上的点的坐标特点”这一基础知识,在三张完全相同且不透明的卡片正面分别写上了﹣3,0,2三个数字,背面向上洗匀后随机抽取一张,将卡片上的数字记为a,再从剩下的两张中随机取出一张,将卡片上的数字记为b,然后叫万宇在平面直角坐标系中找出点M(a,b)的位置.
(1)请你用树状图帮万宇同学进行分析,并写出点M所有可能的坐标;
(2)求点M在第二象限的概率;
(3)张老师在万宇同学所画的平面直角坐标系中,画了一个半径为3的⊙O,过点M能作多少条⊙O的切线?请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形 ![]() 中,
中,![]() ,
,![]() ,
,![]() 是矩形
是矩形 ![]() 中能剪出的最大圆,矩形
中能剪出的最大圆,矩形 ![]() 固定不动,
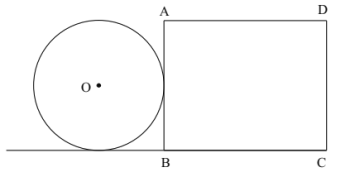
固定不动,![]() 从如图位置开始沿射线
从如图位置开始沿射线 ![]() 方向平移,当
方向平移,当 ![]() 与矩形
与矩形 ![]() 重叠部分面积为
重叠部分面积为 ![]() 面积一半时,平移距离为________________.
面积一半时,平移距离为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)请说出这个几何体模型的最确切的名称是__ __;
(2)如图②是根据 a,h的取值画出的几何体的主视图和俯视图(图中的粗实线表示的正方形(中间一条虚线)和三角形),请在网格中画出该几何体的左视图;
(3)在(2)的条件下,已知h=20 cm,求该几何体的表面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=![]() x+6.
x+6.
(1)求直线y=![]() x+6与x轴、y轴交点坐标;
x+6与x轴、y轴交点坐标;
(2)求出一次函数图象与坐标轴所围成的三角形的面积;
(3)求坐标原点O到直线y=![]() x+6的距离.
x+6的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,工人师傅常用“卡钳”这种工具测定工件内槽的宽.卡钳由两根钢条AA′、BB′组成,O为AA′、BB′的中点.只要量出A′B′的长度,由三角形全等就可以知道工件内槽AB的长度.则判定△OAB≌△OA′B′的依据是( )

A. SASB. ASAC. SSSD. AAS
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com