
【题目】点P到图形Ω(可以是线段、三角形、圆或不规则图形等)的距离是指:点P与图形Ω中所有点连接的线段中最短线段的长度.如图①中的两个虚线段PQ的长度都表示点P到图形Ω的距离.

如图②,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为![]() ,点P从原点出发,以每秒1个单位长度的速度向x轴的正方向运动了t秒.
,点P从原点出发,以每秒1个单位长度的速度向x轴的正方向运动了t秒.

(1)当t=0时,求点P到△ABC的距离;
(2)当点P到△ABC的距离等于线段AP的长度时,求t的范围;
(3)当点P到△ABC的距离大于![]() 时,求t的取值范围.
时,求t的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,P到△ABC的距离等于线段PA的长度;(3)当t>5时,点P到△ABC的距离大于
时,P到△ABC的距离等于线段PA的长度;(3)当t>5时,点P到△ABC的距离大于![]()
【解析】
(1)作AM⊥BC,ON⊥AB,根据A、B、C三点的坐标求出△AMB为等腰直角三角形,继而求出∠OBN=45°,即可得到ON的长度;
(2)过点A分别作AB与AC的垂线,与x轴分别交于点D、E,当P运动到D、E之间时,P到△ABC的距离等于PA的长度,求得AD、AE的长度即可得到取值范围;
(3)由(1)可知P点只能在E点右侧,作PG⊥AC,作GH⊥x轴,利用三角形相似求出G点的横坐标为4,且HP=2FE=1,由此求出t的取值范围.
(1)作AM⊥BC,ON⊥AB,
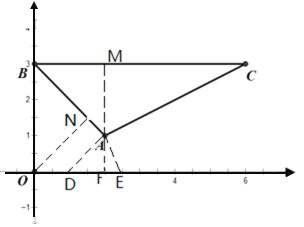
由![]() 得BC∥x轴,
得BC∥x轴,
∴AM=BM=2
∴△AMB为等腰直角三角形,∠ABM=45°
∴∠OBN=45°
∴![]()
(2)作AF⊥x轴,过点A分别作AB与AC的垂线,与x轴分别交于点D、E
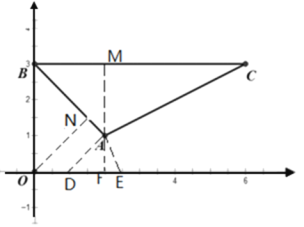
当P运动到D、E之间时,P到△ABC的距离等于PA的长度
△ADF中,∠ADF=45° DF=AF=1,故点D横坐标为1
∵△AFE~△CMA
∴![]()
∴FE=![]() ,故点E的横坐标为
,故点E的横坐标为![]()
∴当![]() 时,P到△ABC的距离等于线段PA的长度
时,P到△ABC的距离等于线段PA的长度
(3)直线AC的方程为![]()
∵![]() ,P点只能在E点右侧,
,P点只能在E点右侧,
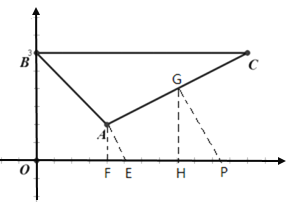
作PG⊥AC,作GH⊥x轴
△AFE~△GHP
![]()
故GH=2,又直线AC的方程为![]()
当y=2时, ![]() 得x=4,
得x=4,
∴G点的横坐标为4,且HP=2FE=1
故点P的横坐标为5
当t>5时,点P到△ABC的距离大于![]()


科目:初中数学 来源: 题型:
【题目】某大学毕业生响应国家自主创业的号召,投资开办了一个装饰品商店,某种商品每件的进价为20元,现在售价为每件40元,每周可卖出150件,市场调查发现:如果每件的售价每降价1元(售价不低于20元),那么每周多卖出25件,设每件商品降价![]() 元,每周的利润为
元,每周的利润为![]() 元.
元.
(1)请写出利润![]() 与售价
与售价![]() 之间的函数关系式.
之间的函数关系式.
(2)当售价为多少元时,利润可达4000元?
(3)应如何定价才能使利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
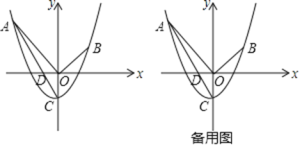
【题目】如图,在平面直角坐标系中,抛物线![]() ,过点
,过点![]() 和点
和点![]() ,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
![]() 求抛物线
求抛物线![]() 的函数表达式;
的函数表达式;
![]() 求点D的坐标;
求点D的坐标;
![]() 的大小是______;
的大小是______;
![]() 将
将![]() 绕点O旋转,旋转后点C的对应点是点
绕点O旋转,旋转后点C的对应点是点![]() ,点D的对应点是点
,点D的对应点是点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点M,在
交于点M,在![]() 旋转过程中,当点M与点
旋转过程中,当点M与点![]() 重合时,请直接写出点M到AB的距离.
重合时,请直接写出点M到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b的图象与反比例函数![]() 的图象相交于A(﹣1,m),B(n,-1)两点.
的图象相交于A(﹣1,m),B(n,-1)两点.
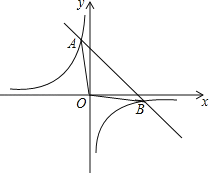
(1)求出这个一次函数的表达式;
(2)求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
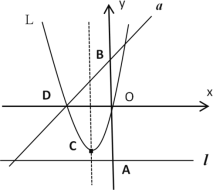
【题目】如图,若m是正数,直线l:y=-m与y轴交于点A;直线a:y=x+m与y轴交于点B;抛物线L:y= x2+mx的顶点为C,且L与x轴左交点为D.
(1)若AB=12,求m的值,此时在抛物线的对称轴上存在一点P使得△![]() 的周长最小,求点P坐标;
的周长最小,求点P坐标;
(2)当点C在直线l上方时,求点C与直线l距离的最大值;
(3)在抛物线L和直线a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出m=2020和m=2020.5时“美点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com