
����Ŀ����ͼ����m��������ֱ��l��y����m��y�ύ�ڵ�A��ֱ��a��y��x+m��y�ύ�ڵ�B��������L��y�� x2+mx�Ķ���ΪC����L��x����ΪD��
��1����AB��12����m��ֵ����ʱ�������ߵĶԳ����ϴ���һ���ʹ�á�![]() ���ܳ���С���������ꣻ
���ܳ���С���������ꣻ
��2������C��ֱ��l�Ϸ�ʱ�����C��ֱ��l��������ֵ��
��3����������L��ֱ��a��Χ�ɵķ��ͼ�εı߽��ϣ��Ѻᡢ�����궼�������ĵ��Ϊ�����������ֱ�ֱ��д��m��2020��m��2020.5ʱ���������ĸ�����
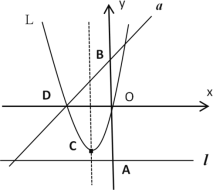
���𰸡���1��P����3��3 ������2����C��l��������ֵΪ1����3��m��2020ʱ���������ĸ���Ϊ4042����m��2020.5ʱ���������ĸ���Ϊ1011��
��������
�⣺��1�����A��B�����꣬�ֱ�ΪA��0����m����B ��0��m������AB��8�����ɵõ�m������m����12���������m.��֪�ϡ���������ڶԳ���Գ�ʱ����OP=DPʱ��OB+OP+PB=OB+DP+PB ��B��P��D������ʱ��![]() �ܳ���̣����P�����꼴��.
�ܳ���̣����P�����꼴��.
��2�������κ���תΪ����ʽ��y����x+ ![]() ��2��
��2��![]() �����������C
�����������C
C��l�ľ���![]() ��1���ݴ˿��жϳ�������.
��1���ݴ˿��жϳ�������.
��3���ֱ������m��2020ʱ���뵱m��2020.5ʱ�����������߽���ʽ��ֱ�߽���ʽ����������꣬�����������µĵ�����������ɣ�ע��������ۡ�
�⣺��1����x��0����y��x+m��m��
��B ��0��m����
��AB��8����A��0����m����
��m������m����12��
��m��6��
��L��y��x2+6x��
��L�ĶԳ���x����3��
��֪�ϡ���������ڶԳ���Գƣ���OP=DP
��OB+OP+PB=OB+DP+PB ��B��P��D������ʱ��![]() �ܳ���̣���ʱ��PΪֱ��a��Գ���Ľ��㣬��x����3����y��x+6��3��
�ܳ���̣���ʱ��PΪֱ��a��Գ���Ľ��㣬��x����3����y��x+6��3��
��P����3��3 ��
��2��y����x+ ![]() ��2��
��2��![]() ��
��
��L�Ķ���C
�ߵ�C��l�Ϸ���
��C��l�ľ���![]() ��1��
��1��
���C��l��������ֵΪ1
��3����m��2020ʱ������4042�����㣬��m��2020.5ʱ������1011�����㡣
�ٵ�m��2020ʱ�������߽���ʽL��y��x2+2020x
ֱ�߽���ʽa��y��x+2020
����������������ʽ�ɵã�x1����2020��x2��1��
���֪ÿһ������x��ֵ ����Ӧ��һ������yֵ���ҩ�2020��1֮�䣨������2020��1������2022��������
������Ҫ֪����Χ�ɵķ��ͼ�α߽�������֣��߶κ������ߣ�
���߶κ��������ϸ���2022��������
���ܼ�4044���㣬
��������ͼ����2�����ظ��ظ���
���������ĸ�����4044��2��4042��������
�ڵ�m��2020.5ʱ��
�����߽���ʽL��y��x2+2020.5x��
ֱ�߽���ʽa��y��x+2020.5��
����������������ʽ�ɵã�x1����2020.5��x2��1��
�൱xȡ����ʱ����һ�κ���y��x+2020.5�ϣ�yȡ��������ֵ������ڸ�ͼ������������Ϊ0��
�ڶ��κ���y��x2+2020.5xͼ���ϣ���xΪż��ʱ������ֵy��ȡ������
��֪��2020.5��1֮����1010��ż���������ک�2020.5��1֮�仹������0����֤���֪0Ҳ����
���������������������1011����
��m��2020ʱ���������ĸ���Ϊ4042����m��2020.5ʱ���������ĸ���Ϊ1011��


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
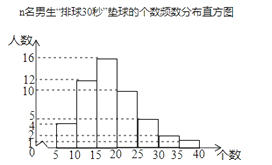
����Ŀ��ijУΪ��Ԥ����꼶����������30������ǽ�����������ӱ�У���꼶�����ȡ��n���������и���Ŀ���ԣ������Ƴ����µ�Ƶ���ֲ�ֱ��ͼ�����д��������η�Ϊ�߸��飨ÿ�麬��Сֵ���������ֵ��������ͳ��ͼ�ṩ����Ϣ����������⣺
��1����n��ֵ��
��2������������ݵ���λ�����ڵڼ��飿
��3�������Ծ��꼶����������30������ǽ�������������10��Ϊ�ϸ���ͳ�ƽ�������Ƹ�У���꼶450����ͬѧ�ɼ��ϸ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ���ۺ�ʵ�������ţ��ƻ�����![]() ����դ�����ϣ�һ�߿�ԭ�о�ǽΧ����ͼ��ʾ���������������ǽ�ij���Ϊ
����դ�����ϣ�һ�߿�ԭ�о�ǽΧ����ͼ��ʾ���������������ǽ�ij���Ϊ![]() .
.
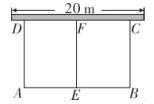
��1���ܷ�Χ�������Ϊ![]() ����������ܣ����
����������ܣ����![]() �ij��ȣ������ܣ�˵�����ɣ�
�ij��ȣ������ܣ�˵�����ɣ�
��2���ܷ�Χ�������Ϊ![]() �������˵˵�������.
�������˵˵�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Σ����ǵ��������Σ�һ����������һ��������Ա��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ָ��ߣ�
��1����ͼ����![]() �У�CDΪ��ƽ���ߣ�
�У�CDΪ��ƽ���ߣ�![]() ��
��![]() ����֤��CDΪ
����֤��CDΪ![]() �������ָ��ߣ�
�������ָ��ߣ�

��2����ͼ��![]() �У�
��![]() ��
��![]() ��CD��
��CD��![]() �������ָ��ߣ���
�������ָ��ߣ���![]() ����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
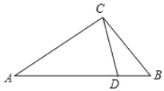
��3����![]() ��
��![]() ��CD��
��CD��![]() �������ָ��ߣ���
�������ָ��ߣ���![]() Ϊ���������Σ�ֱ��д����ACB�Ķ�����
Ϊ���������Σ�ֱ��д����ACB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���ͼ1����O��������ABCD���Խ��ߵĽ��㣬�ֱ��ӳ�OD����G��OC����E��ʹOG=2OD��OE=2OC��Ȼ����OG��OEΪ�ڱ���������OEFG������AG��DE��

��1����֤��DE��AG��
��2��������ABCD�̶�����������OEFG�Ƶ�O��ʱ����ת���ǣ�0��������360�����õ�������OE��F��G������ͼ2��
������ת�����У�����OAG����ֱ��ʱ�������Ķ�����
����������ABCD�ı߳�Ϊ1������ת�����У���AF���������ֵ�ʹ�ʱ���Ķ�����ֱ��д���������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��ͼ�������������߶Ρ������Ρ�Բ����ͼ�εȣ��ľ�����ָ:��P��ͼ���������е����ӵ��߶�������߶εij���.��ͼ���е��������߶�PQ�ij��ȶ���ʾ��P��ͼ�����ľ���.

��ͼ�ڣ���ƽ��ֱ������ϵxOy�У���ABC��������������ֱ�Ϊ![]() ����P��ԭ���������ÿ��1����λ���ȵ��ٶ���x����������˶���t��.
����P��ԭ���������ÿ��1����λ���ȵ��ٶ���x����������˶���t��.

��1����t=0ʱ�����P����ABC�ľ��룻
��2������P����ABC�ľ�������߶�AP�ij���ʱ����t�ķ�Χ��
��3������P����ABC�ľ������![]() ʱ����t��ȡֵ��Χ.
ʱ����t��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y��ax2+bx+c��a��0���ĶԳ���Ϊx����1���������߾��� A��1��0����C��0��3�����㣬��x�ύ�ڵ�B��
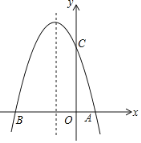
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ���x����1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�����ʱ��M�����ꣻ
��3�����PΪ�����߶Գ���x����1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˿�չ�����������˶������ƻ��������������.��֪����20�������40��������ܽ��Ϊ4600Ԫ������30�������50��������ܽ��Ϊ6100Ԫ.
��1��ÿ������ÿ������ļ۸�ֱ�Ϊ����Ԫ��
��2������У�������������60�����ҹ���������ܽ���������������ܽ����У���ɹ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������CD��AB����CDB��30�㣬CD��6����Ӱ����ͼ�ε����Ϊ�� ��
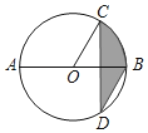
A. 4��B. 3��C. 2��D. ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com