
| A. | $\sqrt{24}$ | B. | $\sqrt{32}$ | C. | $\sqrt{40}$ | D. | $\sqrt{\frac{3}{4}}$ |
分析 先把各选项化成最简二次根式,然后根据同类二次根式的定义选择即可.
解答 解:A、$\sqrt{24}$=2$\sqrt{6}$,与$\sqrt{2}$不能合并,故本选项错误;
B、$\sqrt{32}$=4$\sqrt{2}$,与$\sqrt{2}$能合并,故本选项正确;
C、$\sqrt{40}$=2$\sqrt{10}$,与$\sqrt{2}$不能合并,故本选项错误;
D、$\sqrt{\frac{3}{4}}$=$\frac{\sqrt{3}}{2}$,与$\sqrt{2}$不能合并,故本选项错误.
故选B.
点评 此题主要考查了同类二次根式的定义,即:二次根式化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{4}$ | C. | $\sqrt{8}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源:2017届四川省广安市岳池县九年级第二次诊断考试数学试卷(解析版) 题型:判断题
已知:二次函数 的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
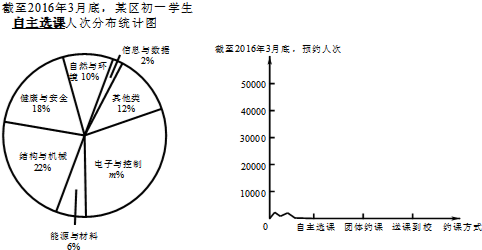
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.0×105 | B. | 30×104 | C. | 3.0×104 | D. | 3.0×101 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com