
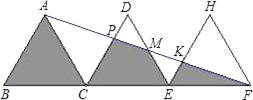
【题目】如图,△ABC、△DCE、△HEF、是三个全等的等边三角形,点B、C、E、F在同一条直线上,连接AF,与DC、DE、HE分别相交于点P、M、K,若△DPM的面积为2,则图中三个阴影部分的面积之和为_____.
【答案】26
【解析】
根据全等三角形对应角相等,可以证明AC∥DE∥HF,再根据全等三角形对应边相等BC=CE=EF,然后利用平行线分线段成比例定理求出AB=3KE,PC=2KE,得出△DMP≌△EMK,S△MEK=2,M是DE的中点,再由相似三角形的性质即可得出答案.
∵△ABC≌△DCE≌△HEF,
∴∠ACB=∠DEC=∠HFE,BC=CE=EF,
∴AC∥DE∥HF,
![]() ,
,![]()
∴AB=3KE,PC=2KE,
∴PD=KE,
∵∠D=∠MEK,∠DMP=∠EMK,
∴△DMP≌△EMK,
∴S△MEK=2,M是DE的中点,
∴S△EFK=2S△EMK=4,
∵△EFK∽△CFP,相似比为1:2,
∴S四边形PCEM=S△PCF﹣S△EFK﹣S△MEK=16﹣4﹣2=10,
∴S△ABC=10+2=12,
∴三个阴影部分面积=S△ABC+S四边形PCBM+S△EFK=12+10+4=26.
故答案为26.


科目:初中数学 来源: 题型:
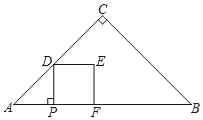
【题目】如图,在△ABC中,∠C=90°,AC=BC,AB=8.点P从点A出发,以每秒2个单位长度的速度沿边AB向点B运动.过点P作PD⊥AB交折线AC﹣CB于点D,以PD为边在PD右侧做正方形PDEF.设正方形PDEF与△ABC重叠部分图形的面积为S,点P的运动时间为t秒(0<t<4).
(1)当点D在边AC上时,正方形PDEF的边长为 (用含t的代数式表示).
(2)当点E落在边BC上时,求t的值.
(3)当点D在边AC上时,求S与t之间的函数关系式.
(4)作射线PE交边BC于点G,连结DF.当DF=4EG时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
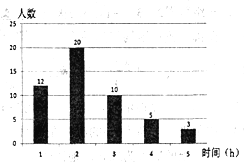
【题目】在创建“书香校园”活动中,为了解学生的读书情况,某校抽样调查了部分同学在一周内的阅读时间,绘制如下统计图.根据图中信息,解答下列问题:
(1)被抽查学生阅读时间的中位数为_______h,众数为________h;平均数为________h:
(2)若该校共有800名学生,请你估算该校一周内阅读时间不少于3h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,等腰Rt△OAB的一条直角边OA 在x轴的正半轴上,点B在双曲线![]() 上,且∠BAO=90°,
上,且∠BAO=90°,![]() .
.
(1)求k的值及点A的坐标;
(2)△OAB沿直线OB平移,当点A恰好在双曲线上时,求平移后点A的对应点A′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是圆O的直径,AB、AD是圆O的弦,且AB=AD,连接BC、DC.
(1)求证:△ABC≌△ADC;
(2)延长AB、DC交于点E,若EC=5 cm,BC=3 cm,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
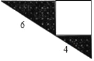
【题目】如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
A. 3![]() B. 9 C. 12 D. 24
B. 9 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年12月16﹣18日,第二届互联网大会在浙江乌镇胜利举行,这说明我国互联网发展走到了世界的前列,尤其是电子商务.据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)当销售单价定为50元时,求每月的销售件数;
(2)设每月获得利润为w(元),求每月获得利润w(元)关于销售单价x(元)的函数解析式;
(3)由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月获得的利润不低于8000元,那么每月的成本最少需要多少元?(成本=进价×销售量)

查看答案和解析>>
科目:初中数学 来源: 题型:
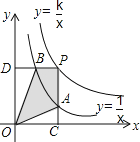
【题目】反比例函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴,交y=
的图象上,PC⊥x轴,交y=![]() 的图象于点A,PD⊥y轴,交y=
的图象于点A,PD⊥y轴,交y=![]() 的图象于点B.当点P在y=
的图象于点B.当点P在y=![]() 的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
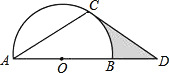
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com